Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 40
Determine a força no elemento .
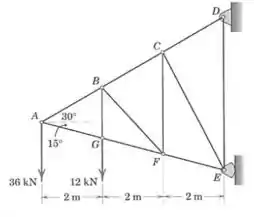
Passo 1
Vamos começar olhando para um seção da treliça que vai até os pontos e :
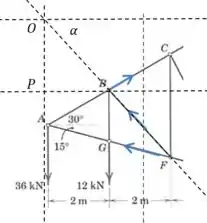
E então vamos procurar uma expressão para o ângulo (dê uma olhada no desenho!):
Passo 2
Agora vamos montar uma equação de equilíbrio para o momento em torno do ponto , já que nesse caso vamos excluir as forças , e a força em :
E lembrando que :
Passo 3
E então falta encontrar uma expressão para . Vamos usar o nosso desenho para isso:
Já que o ângulo também está em :
E agora vamos substituir isso na expressão que tínhamos encontrado antes:
Resposta
A força é .
Exercícios de Livros Relacionados
Calcule as forças nos elementos C B , C G e F G da treliça carregada, sem calcular primeiro a força em qualquer outro elemento.
Determine as forças nos elementos D E ,D L , L M e E L da treliça simétrica carregada.
Determine a força no elemento J M da treliça carregada.
Os quadros articulados A C E e D F B estão ligados por duas barras articuladas, A B e C D , que se cruzam sem estarem interligadas. Calcule a força em A B .
Determine as forças nos elementos D E ,E I , F I e H I da treliça em arco de um telhado.