Calcule a força no elemento da treliça carregada.
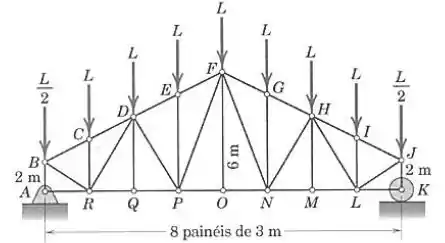
Passo 1
Como estamos interessados na força em , vamos aplicar o método das seções nesse trecho da treliça:
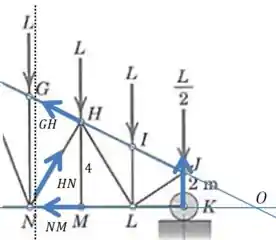
Nosso objetivo é calcular a força , então vamos escrever o momento em relação ao ponto , pois assim as forças e terão momento nulo.
Já vimos que para cada “passo” de na horizontal, a treliça “desce” na vertical. Então a distância de até (que estão separados por na vertical) é de .
Onde ) é o seno do ângulo que forma com a horizontal. O já está representado no desenho, e podemos calcular o usando o teorema de pitágoras.
Passo 2
Agora vamos resolver essa equação:
E fica faltando encontrar o valor de . Mas dê uma olhada na figura do enunciado. A carga total de força sobre a treliça (vindo de cima) é:
Pela simetria da treliça, podemos deduzir que a força suportada em e em são iguais, ou seja:
E substituindo isso na equação:
Resposta
A força é .