Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 141
Resolva o Problema 4.141 considerando que o arame DF é substituído por um arame que conecte C e F
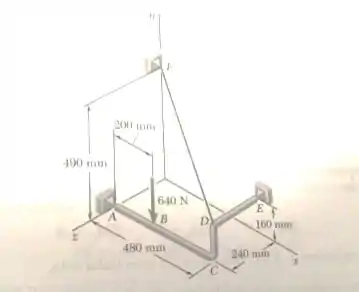
Figura P.140
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Precisamos determinar a tração (que chamaremos de ) considerando que agora ele é ligado de C para F
Olhando para a imagem do enunciado, podemos notar que todas as forças estão em (Newtons) e todas as medidas estão em mm (milímetros). Portanto, não precisaremos converter unidades e as reações serão encontradas em .
Passo 2
Agora consideraremos o seguinte diagrama de corpo livre:
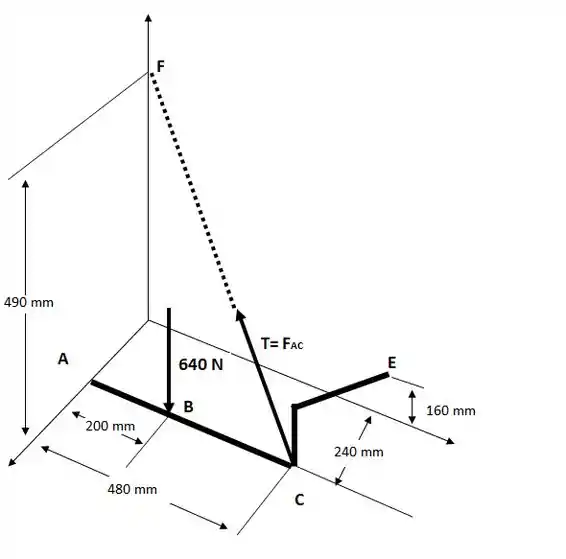
Consideraremos o somatório dos momentos em torno da linha AE (vetor )
:
=0
Passo 3
Determinaremos todos os vetores na relação resultante do somatório dos momentos demonstrada no passo anterior. Começando pelo vetor unitário da direção AE
Determinaremos agora o vetor :
vetor :
vetor :
Agora encontraremos a relação para o vetor . Como não conhecemos a sua magnitude, ele será escrito como como um produto de T (incógnita) pelo vetor unitário na sua direção, que pode ser determinado pelas medidas de comprimento.
Passo 4
Substituiremos agora os vetores encontrados no passo 3 na relação encontrada no passo 2: