Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 85
Determine a força que as garras do cortador de metal exercem sobre o cabo liso se forem aplicadas forças de 100 N aos punhos. As garras possuem pinos em e , e em e . Também há um pino em .
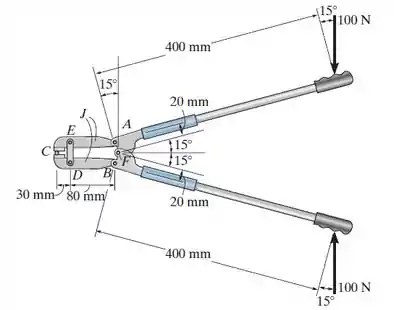
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão que parece ser bem difícil devido a geometria do problema. Temos que determinar a força normal que o cortador faz em .
Para isto, vamos ter que trabalhar com duas partes. Vamos ter de analisar o diagrama de corpo livre no braço que contém os pinos e e que aplica a força de . Aqui obteremos a reação em , que é fundamental para resolver a questão.
Após determinarmos a reação em , podemos determinar a força normal em analisando o diagrama de corpo livre no membro .
Sendo assim, vamos esboçar os diagramas de corpo livre. Relembrando, só devemos tomar muito cuidado ao colocarmos forças que aparecem em dois componentes! Pela lei de ação e reação, elas terão um sentido oposto!
Sendo assim, começando pelo membro em que atua a força de , temos:
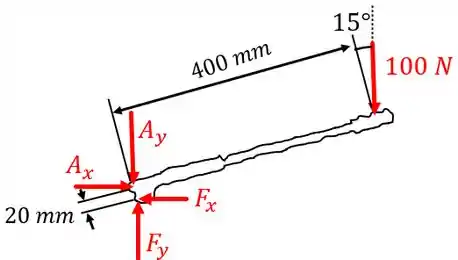
Já para o membro , temos:
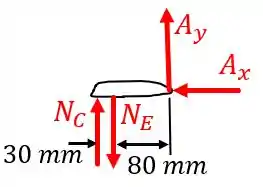
Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
Temos que começar determinando as reações no pino em . Se começarmos analisando o membro , a única força horizontal é . Portanto, já podemos afirmar que:
Agora podemos voltar para o membro em que atua a força de para determinar . Fazendo o somatório de momentos em torno do ponto , temos:
Passo 3
Agora que temos todas as reações no pino , podemos determinar a força normal no ponto .
Para isto, basta fazermos o somatório de momentos em torno do ponto , temos:
E assim finalizamos a questão!