Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 80
A lança é sustentada por uma junta esférica em A e um fio tirante em B. Se as cargas de 5 kN se
situam em um plano paralelo ao plano x–y, determine as componentes x, y, z da reação em A e a tração no cabo em B.
Passo 1
Oi, tudo bem? Vamos analisar esta questão.
Primeiro devemos construir um diagrama de corpo livre e descobrir o valor das reações de apoio. Temos que:
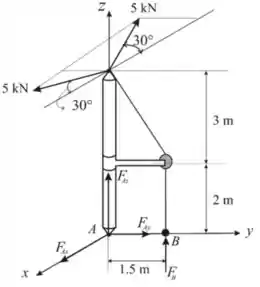
Considerando o equilíbrio em , temos que:
Para a componente em , temos que:
Para a componente em , temos que:
Considerando o momento ao longo de , temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
A placa de aço quadrada tem massa de 1800k g com centro de massa em seu centro G . Calcule a tensão em cada um dos três cabos com os quais a placa é levantada enquanto permanece na horizontal.
O pino em O pode suportar uma força máxima de 3,5k N . Qual é a carga máxima L correspondente que pode ser aplicada ao colchete angular A O B ?
Por causa de uma combinação das condições de suporte do solo e da tensão no cabo de alimentação único, o poste desenvolveu a inclinação de 5 ° indicada. O poste uniforme de 9m tem uma massa por unidad
O suporte grande é construído em chapa pesada que possui massa ρ por unidade de área. Determine as reações de força e momento no parafuso de suporte em O .
O alçapão uniforme de 30 por 40i n pesa 200l b e é mantido aberto pelo suporte leve A B no ângulo θ = tan - 1 4 3 . Calcule a compressão F B na biela e a força suportada pela dobradiça D normal ao e