Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 84
A tenaz de dupla garra suporta a bobina com massa de 800 kg e centro de massa em . Determine as componentes horizontal e vertical das forças que os membros articulados exercem sobre a placa nos pontos e . A bobina exerce apenas reações verticais em e .
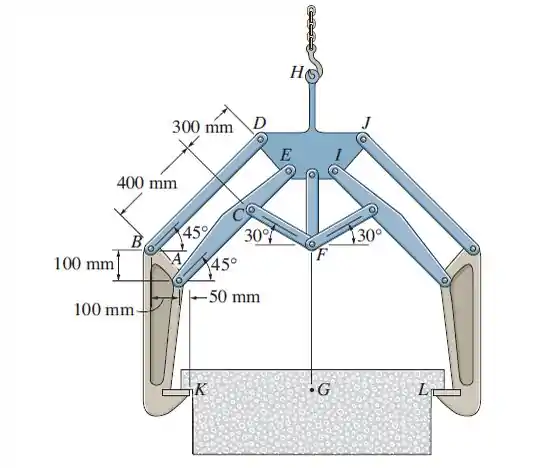
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão que parece ser bem difícil devido a geometria do problema. Entretanto, ela é bem tranquila. A simetria ajuda bastante!
Por exemplo, quem é a força normal em e em ? Elas são iguais a metade do peso! A simetria do problema implica que .
E este é o nosso ponto de partida. Queremos determinar as componentes horizontal e vertical das reações em e . Para isto, vamos ter de analisar três membros: , e .
Desta forma, vamos precisar desenhar o diagrama de corpo livre dos membros e .
Mas e o ? Não é necessário? E a resposta é que, neste caso, não é. Como é uma barra simples, as componentes em são exatamente as componentes de que obtermos no membro !
Então, vamos aos esboços do diagrama de corpo livre. Começando por , temos:
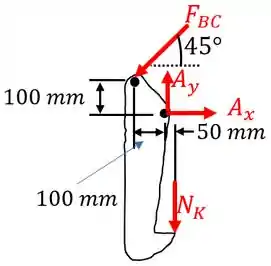
Já para o membro , temos:
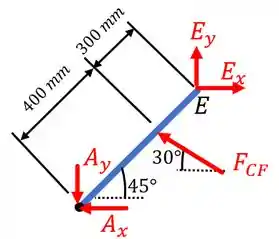
Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
Vamos começar trabalhando com o membro . Para isto, vamos fazer o somatório dos momentos em torno do ponto , pois assim eliminamos esta reação da nossa equação.
Desta forma, temos:
As reações em serão:
Já para calcularmos as reações em , temos que fazer o somatório de forças em ambas as direções vertical e horizontal. Portanto,
Resolvendo o sistema acima obtemos:
Passo 3
Para finalizarmos a questão, temos que determinar as reações horizontal e vertical aplicadas no pino em . Para isto, vamos analisar o membro .
Fazendo o somatório dos momentos em torno do ponto , pois assim eliminamos esta reação da nossa equação, temos:
Agora, fazendo o somatório de forças em ambas as direções vertical e horizontal, temos:
Resolvendo o sistema acima obtemos:
E assim finalizamos a questão!