O dispositivo “mandíbulas da vida” de Prob. 4/88 é redesenhado aqui com suas mandíbulas abertas. A pressão atrás do pistão P de área de 20 in² é mantida em Calcule e plote a força R como uma função de θ para 0≤θ≤ 45∘, onde R é a força vertical atuando nos destroços conforme mostrado. Determine o valor máximo de R e o valor correspondente do ângulo da mandíbula. Veja a figura do Prob. 4/88 para dimensões e a geometria associada à condição θ = 0. Observe que o elo AB e sua contraparte são ambos horizontais na figura para θ = 0, mas não permanecem horizontais quando as mandíbulas se abrem.
Passo 1
Neste problema, é essencial entender como o dispositivo funciona
Primeiro, vamos desenhar a mandíbula inferior com o membro AB anexado a ela no momento θ = 0 ∘
Podemos notar que o comprimento BC é
E isso faz com que o ângulo do eixo y de

Passo 2
Quando o dispositivo funciona, o ponto C não se move, o ponto B gira em torno de C, portanto, B encontra-se no círculo com centro em C (rad com um raio de ) enquanto o ponto A se move horizontalmente, e desde ele é anexado por 2” membro a B e fica na interseção do círculo com o centro em B (com um raio de r = 2 ") e o eixo horizontal 4 '' acima de C
A etapa final da animação GIF é colocada na linha abaixo, onde determinaremos o ângulo que força F faz com o eixo x
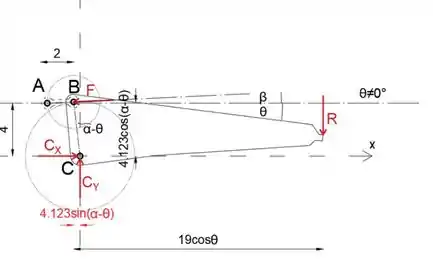
Passo 3
Olhando para a mandíbula inferior isolada, podemos ver que a força no membro AB faz com o ângulo do eixo x de

Passo 4
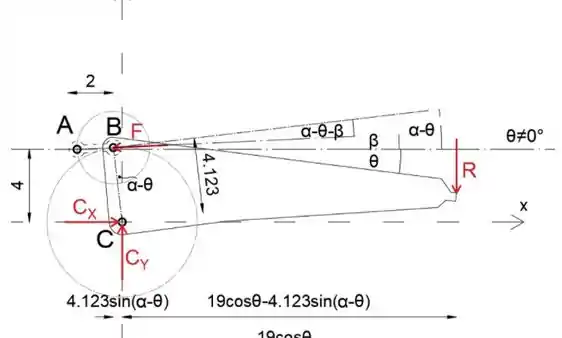
Ao igualar a soma dos momentos sobre o ponto C a zero, eliminaremos as forças de reação em C, para que possamos determinar a força R
Quando substituímos α por seu valor e β pela expressão (1), obteremos a expressão de R em função da força F e do ângulo θ
(2)
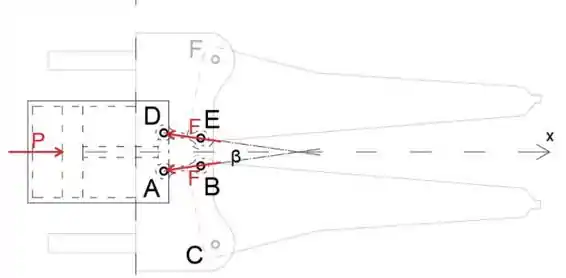
Desenhando o diagrama de corpo livre da parte P com as forças de dois membros atuando nela, podemos determiná-los
Usando simetria, sabemos que as forças nos membros AB e CD são iguais, enquanto a força exercida no dispositivo por pressão é
Passo 5
Ao igualar a soma das forças na direção x a zero, podemos determinar a força F
Passo 6
Finalmente, vamos substituir F na equação (2) pela expressão (3) para obter a expressão de R como função do ângulo θ
Usando uma calculadora gráfica como o Desmos, podemos ver que a força máxima é