Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 33
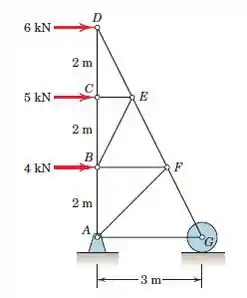
Determine a força no membro BE da treliça carregada.
Passo 1
O enunciado pede que a gente determine a força no membro BE da treliça carregada.
Olhando para a treliça como um todo, podemos ver que o comprimento de CE é 1 "" m (AG é 3m, BF é 2m) e desse comprimento de DE é m. Além disso, o ângulo entre DE e CD é de (do triângulo CDE).
Passo 2
Cortamos CB, BE e EF. Esta seção cortada deve estar em equilíbrio. Observamos o momento sobre D de todas as forças externas (os membros que cortamos agora agem como forças externas).
As forças BC e EF são colineares com o vetor de distância, então seu momento é 0.
Resposta
Exercícios de Livros Relacionados
Cada um dos pontos de apoio B, C, D, E e F é considerado como tendo um contato simples e sem atrito com a superfície de apoio horizontal. Para a carga vertical L mostrada, quais seriam as forças em to
A treliça espacial tetraédrica tem uma base horizontal ABC na forma de um triângulo isósceles e pernas AD BD e CD que suportam a massa m do ponto D. Cada vértice da base é suspenso por um fio vertical
Determine as forças nos membros AD e DG
A treliça espacial mostrada é presa aos suportes fixos em A, B e E e é carregada pela força L que tem componentes xey iguais, mas nenhum componente z vertical. Mostre que há um número suficiente de me
Uma treliça espacial é construída na forma de um cubo com seis membros diagonais mostrados. Verifique se a treliça está internamente estável. Se a treliça está sujeita às forças compressivas P