Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 67

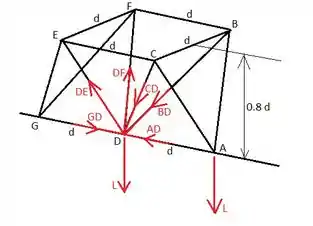
Determine as forças nos membros AD e DG

Passo 1

Olhando para o ponto A, vemos que os membros AB e AC são simétricos e que seu comprimento é:

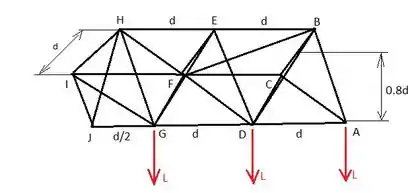
[[| A B | = sqrt(( 0.5 )^2 + ( 0.5 )^2 + ( 0.8 )^2) d],[= 1.0677 d],[| A C | = sqrt(( 0.5 )^2 + ( 0.5 )^2 + ( 0.8 )^2) d],[= 1.0677 d]]

Os componentes Z de AB e AC são iguais e podem ser escritos como a proporção de seu componente z e seu comprimento:

[[A B_z = A B (0.8)/(1.0677)],[A C_z = A C (0.8)/(1.0677)]]

Passo 2

Como o ponto A está em equilíbrio e as forças AC e AB são iguais, podemos escrever:

sum F_z = 0

[[A C (0.8)/(1.0677) + A B (0.8)/(1.0677) = L],[A C (0.8)/(1.0677) + A C (0.8)/(1.0677) = L],[A C = (2 L)/(3)],[A B = (2 L)/(3)]]

sum F_y = 0

[[A D + A C (0.5)/(1.0677) + A B (0.5)/(1.0677) = 0],[A D = - A C (0.5)/(1.0677) - A C (0.5)/(1.0677)]]

A D = - 0.625 L

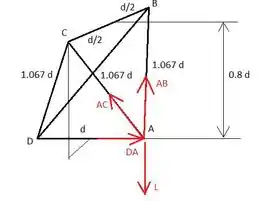
Olhando para o ponto C, podemos ver que apenas as forças (membros) que têm componente Z são AC e CD e, como são simétricas, devem ser iguais. A mesma coisa com o ponto B e os membros AB e BD, eles são iguais

[[B D = A B],[C D = A C],[B D = (2 L)/(3)],[C D = (2 L)/(3)]]

como os membros BD, CD, DE e DF são simétricos e seus componentes z são dados pela mesma fração (já calculamos para AB e AC):

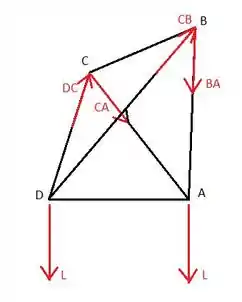
[[B D_z = B D (0.8)/(1.0677)],[C D_z = C D (0.8)/(1.0677)],[D E_z = D E (0.8)/(1.0677)],[D F_z = D F (0.8)/(1.0677)]]

Passo 3

Como o ponto D está em equilíbrio e como DE e DF têm magnitude igual (eles são simétricos), podemos escrever:

sum F_z = 0

[[D E (0.8)/(1.0677) + D F (0.8)/(1.0677) = L + B D (0.8)/(1.0677) + C D (0.8)/(1.0677)],[D E (0.8)/(1.0677) + D E (0.8)/(1.0677) = L + B D (0.8)/(1.0677) + C D (0.8)/(1.0677)],[D E = (4 L)/(3)],[D F = (4 L)/(3)]]

Podemos escrever componentes y dos membros BD, CD, DE e DF como a razão de seu componente y e seu comprimento:

[[B D_z = B D (0.5)/(1.0677)],[C D_z = C D (0.5)/(1.0677)],[D E_z = D E (0.5)/(1.0677)],[D F_z = D F (0.5)/(1.0677)]]

Uma vez que D está em equilíbrio, podemos escrever

B D (0.5)/(1.0677) + C D (0.5)/(1.0677) + D E (0.5)/(1.0677) + D F (0.5)/(1.0677) + A D + D G = 0

D G = - 2.5 L

Resposta

[[A D = - 0.625 L],[D G = - 2.5 L]]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

145- Um dispositivo de abertura de porta é mostrado na figura. As dobradiças com molas em O fornecem um momento K T θ que tende a fechar a porta, onde θ é o ângulo de abertura da porta e a constante d
144- A lança O A do grande guindaste a beira mar pode girar em torno do elemento vertical O B . Determine as forças nos elementos B C e B D e faça seus gráficos em função do ângulo θ - 90 ≤ θ ≤ 90 . A
Determine a força em cada membro da treliça em função da carga P e indique se os membros estão sob tração ou compressão.
Se a força máxima que qualquer membro pode suportar é 4k N em tração e 3k N em compressão, determine a força máxima P que pode ser aplicada ao nó B . Considere d = 1m .
41. A treliça mostrada na figura consiste em 18 elementos e é sustentada por uma rótula em A , duas pequenas hastes de conexão em B e uma pequena haste de conexão em G . ( a ) Verifique se essa treliç