Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 38
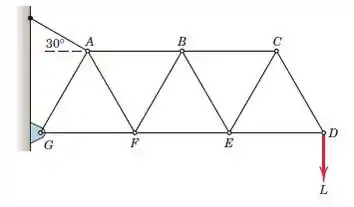
Determine as forças nos membros BC, BE e BF. Os triângulos são equiláteros.
Passo 1
Cortamos BC, BE e EF. Esta seção cortada deve estar em equilíbrio. Primeiro, podemos ver que todos esses triângulos são equiláteros (todos os lados têm o mesmo comprimento, todos os ângulos 60∘). Vamos calcular o momento sobre E de todas as forças externas (agora BC, BE e EF atuam como forças externas).
Passo 2
Agora olhe para o momento sobre D
Agora volte para toda a treliça. Podemos ver que apenas duas forças verticais em B são componentes verticais de BE e BF, portanto, devem ser iguais. Mas, uma vez que eles têm que cancelar, BF é compressão enquanto BE é tensão. BC também é tensão (sendo alongada por força externa).
Resposta
Exercícios de Livros Relacionados
A base de um macaco de automóvel forma um triângulo equilátero de comprimento lateral de 10 pol. E é centralizado sob o colar A. Modele a estrutura como uma com uma esfera e encaixe em cada junta e de
A estrutura representada está sendo considerada como a parte superior de uma torre de linha de transmissão e é apoiada nos pontos F, G, H e I. O ponto C está diretamente acima do centro do retângulo F
Determine as forças nos membros AC e BD da treliça piramidal invertida com base retangular. O ponto M é o ponto médio de BD.
A treliça espacial de Prob. 4/63 é modificado conforme mostrado em que seus suportes e carregamento são alterados. Determine as forças nas barras AC e BD e compare com os resultados do Prob. 4/63.
Para a treliça espacial mostrada, verifique a suficiência dos apoios e também a quantidade e disposição das barras para garantir a determinação estática, tanto externa quanto interna. Por inspeção, de