Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 54
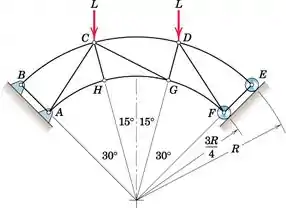
Determine a força no membro BE da treliça carregada.
Passo 1
Se passarmos uma seção pelos membros CD, CG e GH e analisarmos a porção da treliça à esquerda (ou direita), notaremos que existem cinco forças desconhecidas atuando (forças nos membros e força de reação do apoiador em A e B (E e F), portanto, devemos primeiro determinar a força de reação no ponto A e B (ou E e F) a partir do diagrama de corpo livre
Passo 2
Observe que as forças nos membros CD e GH são horizontais, uma vez que os pontos C e D (G e H) são simétricos ao eixo y
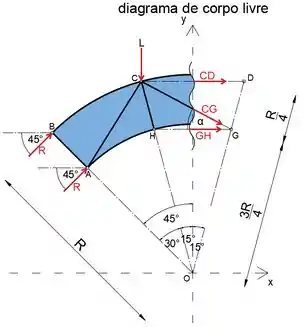
Passo 3
Como sabemos que todas as forças de reação são iguais em magnitude, podemos determiná-las usando uma equação de equilíbrio
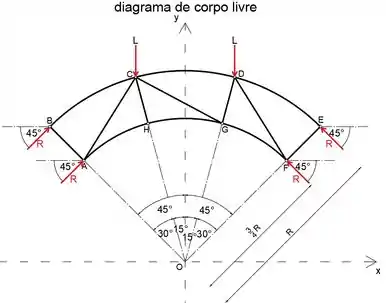
Passo 4
Agora que calculamos os valores das forças de reação, ao olhar para a porção esquerda da treliça, podemos notar que, ao igualar a soma das forças na direção y a zero, a única incógnita será o ângulo a que membro CG machos com eixo z e força CG
Podemos ver que as coordenadas dos pontos C e G são
Passo 5
Distância entre C e G na direção x é
Distância entre C e G na direção y é
Portanto, o ângulo que o membro CG faz com o eixo x é
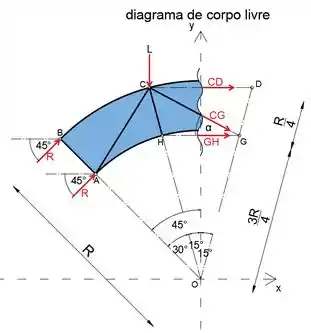
Passo 6
Agora que determinamos o ângulo , podemos determinar a força no membro CG
Vamos supor que todos os membros estão em tensão
Podemos substituir R e a por seus valores