Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 57

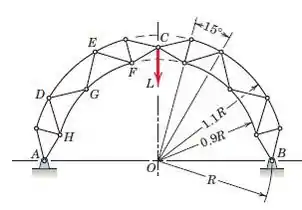
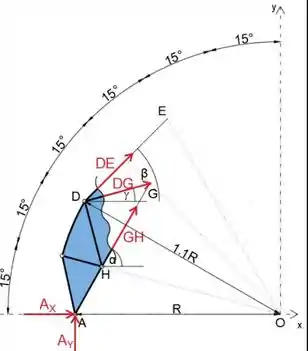
Determine a força no membro DG da treliça composta. Todas as juntas estão em linhas radiais subtendendo ângulos de 15∘ conforme indicado, e os membros curvos agem como membros de duas forças. Distância O C - = O A - = O B - = R .

Passo 1

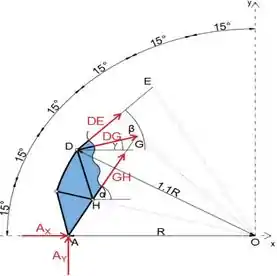
Se passarmos uma seção pelos membros DE, DG e GH e analisarmos a porção da treliça à esquerda, perceberemos que existem cinco forças desconhecidas atuando (forças nos membros e força de reação do apoiador em A), portanto devemos primeiro determine a força de reação no ponto A do diagrama de corpo livre

Passo 2

Equacionando a soma dos momentos sobre o ponto B a zero, podemos determinar a força de reação Ay

∑ M B = 0

A Y ⋅ 2 R - L ⋅ R = 0 A Y = L ⋅ R 2 R A Y = L 2

Passo 3

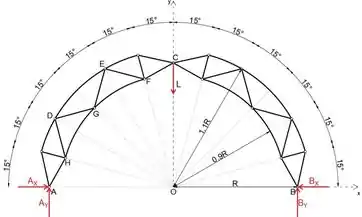
Se passarmos uma seção através das barras perto do ponto C e analisarmos a parte da treliça à esquerda, teremos três forças desconhecidas (força de reação AX e forças de duas barras), portanto, podemos determinar a força de reação AX

∑ M C = 0

A Y ⋅ R - A X ⋅ R = 0 A X = A Y ⋅ R R A X = A Y A X = L 2

Passo 4

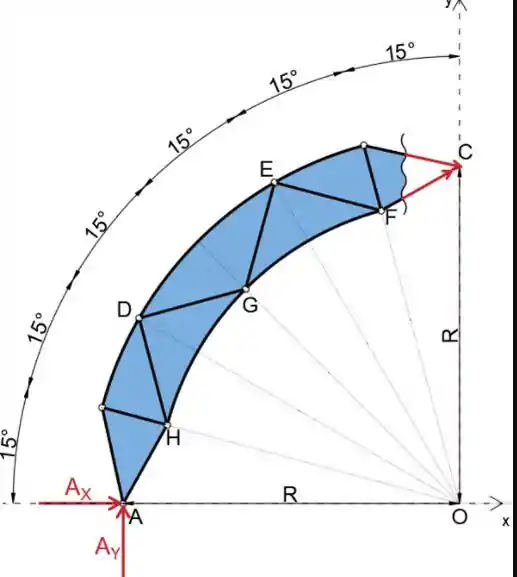
Podemos ver essas coordenadas dos pontos H, G, D e E

H - 0.9 R c o s ⁡ 15 ∘ , 0.9 R s i n ⁡ 15 ∘ G - 0.9 R c o s ⁡ 45 ∘ , 0.9 R s i n ⁡ 45 ∘ D - 1.1 R c o s ⁡ 30 ∘ , 1.1 R s i n ⁡ 30 ∘ E - 1.1 R c o s ⁡ 60 ∘ , 1.1 R s i n ⁡ 60 ∘

Distância entre H e G na direção x é

X | H G | = X G - X H = - 0.9 R c o s ⁡ 15 ∘ - - 0.9 R c o s ⁡ 45 ∘ = 0.2329 R

Distância entre X e G na direção Y é

Y | H G | = Y G - Y H = 0.9 R s i n ⁡ 15 ∘ - 0.9 R s i n ⁡ 45 ∘ = 0.4035 R

Portanto, ângulo com menor membro HG faz com o eixo x

α = t a n - 1 ⁡ 0.4035 R 0.2329 R α = 60 ∘

Passo 5

Distância entre D e G na direção x é

X | D G | = X G - X D = - 0.9 R c o s ⁡ 45 ∘ - - 1.1 R c o s ⁡ 30 ∘ = 0.3162 R

Distância entre D e G na direção y

Y | D G | = Y G - Y D = 0.9 R s i n ⁡ 45 ∘ - 1.1 R s i n ⁡ 30 ∘ = 0.0864 R

Portanto, ângulo com menor membro DE faz com o eixo x

γ = t a n - 1 ⁡ 0.0864 R 0.3162 R γ = 15.28 ∘

Passo 6

Agora que calculamos os valores das forças de reação, passando uma seção pelas barras DE, DG e GH e analisando a parte esquerda da treliça, podemos determinar as forças nessas barras

Distância entre A e D nas direções x e y

X | A D | = X D - X A = - 1.1 R c o s ⁡ 30 ∘ - ( - R ) = 0.0474 R Y | A D | = Y D - Y A = 1.1 R s i n ⁡ 30 ∘ - 0 = 0.55 R

Distância entre D e H na direção x e y

X | D H | = X H - X D = - 0.9 R c o s ⁡ 15 ∘ - - 1.1 R c o s ⁡ 30 ∘ = 0.0833 R Y | D H | = Y H - Y D = 0.9 R s i n ⁡ 15 ∘ - 1.1 R s i n ⁡ 30 ∘ = 0.3171 R

Equacionando a soma dos momentos sobre o ponto D, podemos determinar a força no membro GH

Presumimos que todos os membros estão em tensão

∑ M D = 0

A Y ⋅ X | A D | - A X ⋅ Y | A D | - G H c o s ⁡ α ⋅ Y | D H | - G H s i n ⁡ α ⋅ X | D H | = 0 0.5 L ⋅ 0.0474 R - 0.5 L ⋅ 0.55 R - G H c o s ⁡ 60 ∘ ⋅ 0.3171 R - G H s i n ⁡ 60 ∘ ⋅ 0.0833 R = 0 - 0.2513 L R - 0.2307 R ⋅ G H = 0 G H = - 0.2513 L R 0.2307 R G H = - 1.089 L

Passo 7

Distância entre A e G na direção x e y

X | A G | = X G - X A = - 0.9 R c o s ⁡ 45 ∘ - ( - R ) = 0.3636 R Y | A G | = Y G - Y A = 0.9 R s i n ⁡ 45 ∘ - 0 = 0.6364 R

Distância entre D e G na direção x e y

X | D G | = X G - X D = - 0.9 R c o s ⁡ 45 ∘ - - 1.1 R c o s ⁡ 30 ∘ = 0.3162 R Y | D G | = Y G - Y D = 0.9 R s i n ⁡ 45 ∘ - 1.1 R s i n ⁡ 30 ∘ = 0.0864 R

Equacionando a soma dos momentos sobre o ponto G, podemos determinar a força no membro DE

Presumimos que todos os membros estão em tensão

∑ M G = 0

A Y ⋅ X | A G | - A X ⋅ Y | A G | - D E c o s ⁡ β ⋅ Y | D G | + D E s i n ⁡ β ⋅ X | D G | = 0 0.5 L ⋅ 0.3636 R - 0.5 L ⋅ 0.6364 R - D E c o s ⁡ 45 ∘ ⋅ 0.0864 R + D E s i n ⁡ 45 ∘ ⋅ 0.3162 R = 0 - 0.1364 L R + 0.1625 R ⋅ D E = 0 D E = 0.1364 L R 0.1625 R D E = 0.839 L

Passo 8

Finalmente, ao igualar a soma das forças em x - ou y - direção a zero, podemos determinar a força no membro DG

∑ F X = 0

A X + G H c o s ⁡ α + D E c o s ⁡ β + D G c o s ⁡ γ = 0 D G = - A X + G H c o s ⁡ α + D E c o s ⁡ β cos ⁡ γ D G = - 0.5 L - 1.089 L c o s ⁡ 60 ∘ + 0.839 L c o s ⁡ 45 ∘ cos ⁡ 15.28 ∘ D G = - 0.569 L

Como obtivemos resultado negativo, isso significa que o membro DG está em compressão

D G = 0.569 L C

Resposta

D G = 0.569 L C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma treliça espacial é construída na forma de um cubo com seis membros diagonais mostrados. Verifique se a treliça está internamente estável. Se a treliça está sujeita às forças compressivas P
A seção de treliça piramidal BCDEF é simétrica em relação ao plano vertical x-z, como mostrado. Os cabos AE, AF e AB suportam uma carga de 5 kN. Determine a força no membro BE.
Determine a força (magnitude e direção) que o membro B C exerce no membro A B ( a ) se a carga 900N for aplicada ao centro do membro A B , e ( b ) se a carga 900N for aplicada ao centro do membro B C
Determine os componentes de todas as forças que atuam em cada membro da estrutura carregada.
Determine a magnitude da reação do pino em B ( a ) ignorando o fato de que B D é um membro de duas forças e ( b ) reconhecendo o fato de que B D é um membro de duas forças.