Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 49
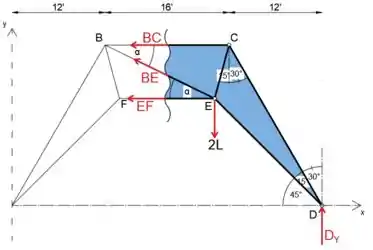
Determine a força no membro BE da treliça carregada.
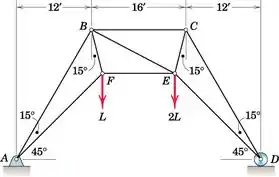
Passo 1
Se passarmos uma seção pelas barras BC, BE e EF e analisarmos a parte da treliça à direita, notaremos que existem quatro forças desconhecidas atuando (forças nas barras e força de reação do apoiador em D), portanto, devemos primeiro determine a força de reação no ponto D do diagrama de corpo livre
Passo 2
Podemos determinar o ângulo que o membro BE faz com o eixo x
Do triângulo CED usando a regra do cosseno, podemos determinar o comprimento do membro CE, uma vez que os comprimentos dos membros CD e DE são
Desde regra
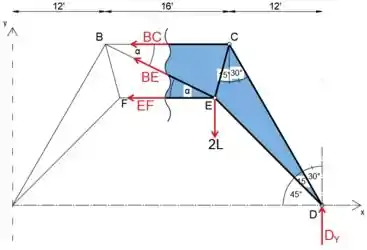
Passo 3
Uma vez que o ângulo BCE é
Usando a regra do cosseno, podemos determinar o comprimento do membro BE
Passo 4
Finalmente, usando a regra seno, podemos determinar o ângulo
Ao igualar a soma dos momentos sobre o ponto A a zero, eliminaremos as forças de reação em A, então a única incógnita na equação será DY
Passo 5
Observe que os membros AF e DE são simétricos, portanto, ambos têm o mesmo comprimento
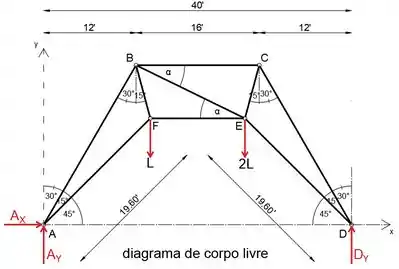
Passo 6
Agora que determinamos a força de reação em D, podemos passar uma seção através dos membros BC, BE e EF e analisar a porção da treliça à direita
Vamos supor que todos os membros estão em tensão
Podemos notar que ambas as forças BC e EF são horizontais, portanto, ao igualar a soma das forças na direção y a zero, podemos determinar a força em menber BE
