Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 55
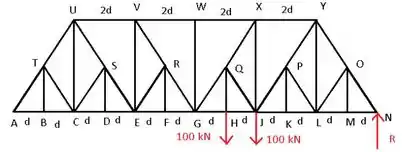
Encontre a força no membro JQ para a treliça de Baltimore onde todos os ângulos são 30∘, 60∘, 90 ∘ ou 120∘.
Passo 1
Podemos encontrar a força de reação no ponto N ao olhar o momento de todas forças externas sobre A
Passo 2
Em seguida, eliminamos WX, GQ e GH. No esboço e , calculando outro terceiro ângulo, obtemos 120∘
Olhando no momento sobre X de forças externas, podemos obter força sobre o membro GH.
Passo 3
Apenas as forças horizontais que atuam em H são GH e JH, portanto, devem ser iguais. Em seguida, fazemos um novo corte em WX, QX, JQ e JH. Ao observar o momento de todas as forças externas sobre X, podemos ignorar as forças WX e QX (não as conhecemos).
Resposta
Exercícios de Livros Relacionados
Para a treliça espacial mostrada, verifique a suficiência dos apoios e também a quantidade e disposição das barras para garantir a determinação estática, tanto externa quanto interna. Por inspeção, de
Cada um dos pontos de apoio B, C, D, E e F é considerado como tendo um contato simples e sem atrito com a superfície de apoio horizontal. Para a carga vertical L mostrada, quais seriam as forças em to
A treliça espacial tetraédrica tem uma base horizontal ABC na forma de um triângulo isósceles e pernas AD BD e CD que suportam a massa m do ponto D. Cada vértice da base é suspenso por um fio vertical
Determine as forças nos membros AD e DG
A treliça espacial mostrada é presa aos suportes fixos em A, B e E e é carregada pela força L que tem componentes xey iguais, mas nenhum componente z vertical. Mostre que há um número suficiente de me