Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 56
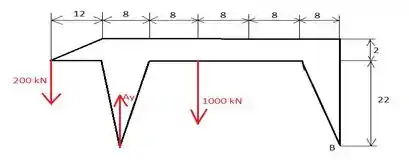
Na ponte rolante mostrada, todos os membros cruzados são tirantes delgados, incapazes de suportar compressão. Determine as forças nas barras DF e EF e encontre a reação horizontal na treliça em A. Mostre que se CF = 0, DE = 0 também.
Passo 1
Primeiro, podemos olhar para toda a estrutura. Uma vez que está em equilíbrio, podemos encontrar a força de reação vertical agindo no ponto A, observando o momento de todas as forças externas agindo sobre B.
aponta para cima
Passo 2
Em seguida, cortamos os membros CE, ED, EF e membros paralelos do EF logo acima. Nosso novo corpo rígido está em equilíbrio. Mesmo que tenhamos feito um corte através de 4 membros, podemos olhar o momento de todas as forças externas (membros cortados agora agem como forças externas) sobre E para obter força naquele membro superior que chamarei de K (o nome não importa)
Passo 3
Em seguida, fazemos um segundo corte (veja a imagem). Mais uma vez, nosso novo corpo rígido está em equilíbrio e podemos olhar no momento em torno de F para obter a componente horizontal da força de reação atuando no ponto A.
aponta para direita
Passo 4
A maneira mais fácil de proceder é observar o que nossas duas forças externas originais estão fazendo com toda a estrutura. É claro que eles estão puxando a estrutura para baixo, mas como não estão agindo no centro da massa, estão produzindo alguma rotação. A força para a esquerda está puxando aquela parte da estrutura para baixo, mas a tensão dos membros não a está deixando, de modo que a força realmente muda de direção, agora puxando a “asa” para baixo e para a direita. A mesma coisa com a força certa. Empurra para baixo e sai por causa da tensão dos membros. Isso causa compressão do membro EF. Mas como esse membro está sendo reduzido, os membros CF e DE estão sendo compactados. Mas como esses membros não suportam compressão, eles não fazem nada. Isso pode parecer uma trapaça para você, mas sentir o que certa força faz ao corpo rígido, como ele está tentando deformá-lo, o ajudará a resolver muitos desses problemas mais rapidamente. Agora podemos fazer um terceiro corte (veja a imagem). Podemos encontrar o ângulo entre vertical e AE.
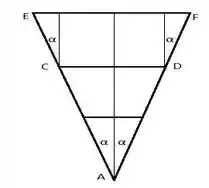
Passo 5
Temos que CF = 0, então temos apenas duas incógnitas, já que calculamos K antes. Este novo corpo está em equilíbrio, podemos olhar no momento em relação a E para obter DF.
Sinal negativo é porque eu desenhei como uma tensão, mas é compressão. A seguir, observe o momento sobre C. Calculamos todas as forças, exceto EF.
Sinal negativo é porque eu desenhei como uma tensão, mas é compressão.