Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 61
Determine a força nos membros , , e da treliça espacial e indique se os membros estão sob tração ou compressão.
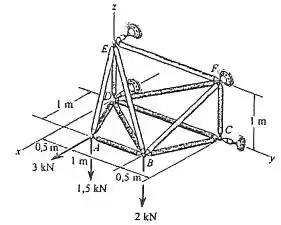
Passo 1
Para determinar as forças, deve-se fazer o diagrama de corpo livre usando o método das juntas de cada junta no qual sejam indicadas todas as forças atuando no respectivo membro.
Para esse caso não é necessário realizar a análise de todos os membros presentes, visto que é pedido para determinar o valor de apenas algumas forças. Isso possibilita fazer praticamente apenas a análise das juntas e pelas forças estarem agindo sobre elas.
Além disso, é conveniente calcular algumas das reações de apoio primeiro visto que as juntas a serem analisadas possuem suportes exercendo forças contrárias a elas.
Passo 2
Primeiramente, então, deve-se fazer o DCL da treliça a fim de determinar as reações. Por conveniência, será adotado um novo sistema de coordenadas com origem na junta . Então, tem-se:
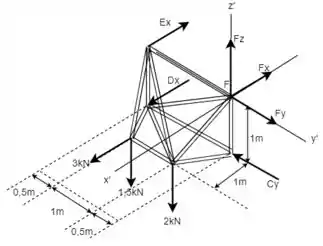
Então, com o DCL é possível montar as equações de equilíbrio para encontrar as reações.
Primeiro, pode-se aplicar o princípio dos momentos em relação ao eixo :
Em seguida, aplicando o mesmo processo para o eixo :
E para o eixo :
E também podem ser feitas as equações de equilíbrio para o eixo :
Para o eixo :
E, enfim, para o eixo :
Passo 3
Agora se torna possível começar a análise das juntas.
Escolhendo a junta primeiro e fazendo o seu DCL, tem-se que:
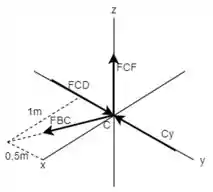
Portanto, a partir destas informações tem-se que para o eixo :
Para o eixo :
E para o eixo :
Como a força age sobre a junta, então ela possui caráter compressivo.
Passo 4
Agora, fazendo o mesmo processo para a junta :
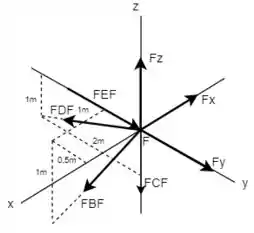
Com isso, é possível montar as equações do equilíbrio de forças para cada eixo.
Então, para o eixo será feito:
Em seguida, para o eixo :
E para o eixo :
Como as forças e agem sobre seus respectivos membros, então possuem caráter trativo.
Já a força possui caráter compressivo por atuar sobre a junta.
Resposta
Junta : , e
Junta : , e