Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 49
49. Determine a força nos membros HI, FI e EF da treliça e diga se os membros estão em tração ou compressão.
Passo 1
Fala aí, galerinha! Pra resolver esse exercício vamos usar o Método das Seções. Mas antes de tudo, vamos encontrar a reação de apoio no ponto G.
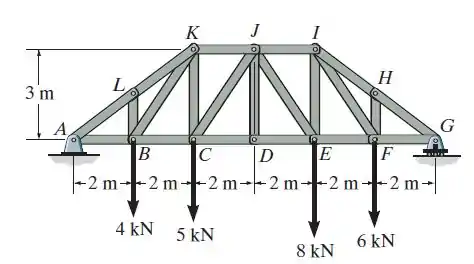
Fazendo o somatório de momentos no ponto A, encontramos a RG, a reação no apoio G.
Passo 2
Agora vamos usar o Método das Seções para calcular os esforços que precisamos, fazendo o somatório de momentos apenas da parte direita da estrutura. No ponto I, temos:
Passo 3
Para fazer o somatório de momentos no ponto G, precisamos definir o ângulo entre as direções FH e FI:
Logo, em G temos:
Passo 4
E por fim, pra achar FHI, vamos fazer o somatório de momentos no ponto F. Pra isso vamos calcular o ângulo entre HI e a direção horizontal:
Então fazendo o somatório de momentos no ponto F, onde a distância entre os pontos H e F é de 1,5m, temos: