Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 57

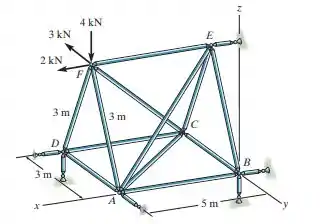
Determine a força nos membros EF, AF e DF da treliça espacial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por elos curtos em A, B, D e E.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Como está a família?? Tudo na paz?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual a força a partir do eixo. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser lembrar que, numa treliça, podemos analisar simetria e os nós. Quando vemos os nós, temos que as forças negativas são de compressão e as positivas de tração, ok?? Então vamos lá...

∑ F x = 0

D x - B x - E x + 2 = 0

∑ F y = 0

A y = 3   k N

∑ F z = 0

D z + B Z - 4 = 0

B z =   - 0,598   k N

Tá, mas agora a gente precisa descobrir nossas variáveis primeiro para cada nó.

∑ M x = 0

4 1,5 + 3 3 sin ⁡ 60 - D z 3 = 0

D z = 4,598   k N

∑ M y = 0

4 5 + 2 3 sin ⁡ 60 - D z 5 - E x 3 sin ⁡ 60 = 0

E x = 0,849   k N

∑ M z = 0

D x 3 + A y 5 - E x 1,5 + 2 1,5 - ( 3 ) ( 5 ) = 0

D x = - 0,5755   k N

B x = 0,5755   k N

Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.

∑ F D z = 0

D z - F D F sin ⁡ 60 = 0

F D F = 5,31   k N

∑ F F x = 0

2 - F E F - 5 34 F C F = 0

∑ F F y = 0

F A F cos ⁡ 60 + 5,31 cos ⁡ 60 - 3 - F C F 1,5 34 = 0

∑ F F z = 0

5,31 sin ⁡ 60 - 4 - F A F sin ⁡ 60 - F C F 3 sin ⁡ 60 34 = 0

Passo 3

Pronto!! Agora vamos jogar tudo lá na nossa formulinha e achar nossos valores!!

F C F = 0

F E F = 2   k N

F A F = 0,691   k N

Resposta

F C F = 0

F E F = 2   k N

F A F = 0,691   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método dos nós, determine a força em cada elemento da treliça mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.
Determine a força em cada membro da treliça Pratt e indique se os membros estão sob tração ou compressão.
Determine a força em cada membro da treliça tesoura dupla em função da carga P e indique se os membros estão sob tração ou compressão.
A força de tração máxima permitida nos membros da treliça é F t m á x = 5k N á , e a força de compressão máxima permitida é F c m á x = 3k N á . Determine a intensidade máxima da carga P que pode ser
A força de tração máxima permitida nos membros da treliça é F t m á x = 5k N á , e a força de compressão máxima permitida é F c m á x = 3k N á . Determine a intensidade máxima P das cargas que podem s