Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 8.Problemas - Ex. 127
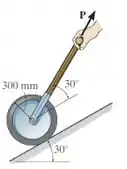
Determine a força necessária para superar a resistência ao rolamento e puxar o cilindro de no plano inclinado com velocidade constante. O coeficiente de resistência ao rolamento é .
Passo 1
Galera, quando um cilindro rígido rola com velocidade constante por uma superfície rígida, a força normal exercida pela superfície sobre o cilindro atua perpendicularmente ao ponto de contato. Mas nós sabemos que nenhum material é perfeitamente rígido e, portanto, a reação da superfície sobre o cilindro consiste em uma distribuição de pressão normal. Conforme ele rola, o material da superfície na frente do cilindro retarda o movimento, pois ele está sendo deformado. Para manter esse movimento constante, é necessária uma força motriz horizontal ser aplicada no cilindro.
Para manter o cilindro em equilíbrio, ou seja, manter ele rolando a uma velocidade constante é preciso que seja concorrente com a força motriz e o peso . Assim, temos a seguinte expressão para esse tipo de situação:
Passo 2
Para começar a resolução dessa questão, vamos desenhar o diagrama de corpo livre para essa situação!
Passo 3
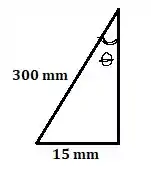
A primeira coisa que podemos fazer nessa questão é descobrir o valor de que está indicado no diagrama de corpo livre. Podemos observar o triângulo abaixo e escrever uma relação trigonométrica para encpntrar o valro de .
Passo 4
Como estamos atuando em um plano inclinado, os nossos eixos de referência serão rotacionados na mesma angulação do plano. O diagrama de corpo livre abaixo mostra como fica a nova situação.
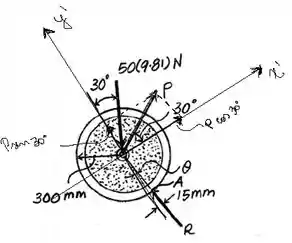
Usando os novos eixos , vamos calcular o somatório das forças verticais e horizontais que, num sistema em equilíbrio, devem ser iguais a zero. Assim,
Temos duas equações com duas incógnitas agora. Se resolvermos esse sistema, nós encontraremos os valores para e !
Resolvendo, encontramos os seguintes valores:
Resposta
A força necessária para superar a resistência ao rolamento é igual a: