Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 104
O tabuleiro da ponte tem um peso por unidade de comprimento de . Ele está apoiado em cada lado por um cabo. Determine a tração em cada cabo nos pilares e .
Passo 1
O problema quer que a gente encontre as trações de cada cabo nos pilares e .
Vamos começar observando um pouco o problema, assim a gente pode fazer um diagrama de corpo livre, assim:
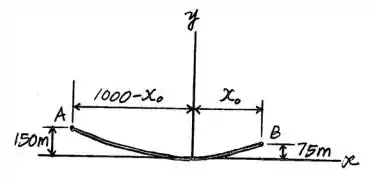
E como a ponte é suportada por dois cabos, a gente acha que:
Passo 2
Nós notamos que na figura do problema, é o ponto mais baixo do cabo, vamos pegar a segunda derivada da equação do cabo, logo:
E integrando isso:
Vamos encontrar , pra isso a gente usa a condição inicial, de que na origem, e então:
Logo é igual a .
Ficamos com:
Integramos mais uma vez para chegamos na função não derivada:
Aplicamos a condição inicial também para descobrirmos :
Encontramos que também é nulo. Então, ficamos com a função do cabo como sendo:
Passo 3
Agora, descobrir pra isso, vamos usar a equação que encontramos nos pontos que já sabemos:
e :
Na equação:
Agora no ponto e , que fica na equação:
Usando essas duas equações como um sistema, encontramos:
Então, substituímos na equação derivada:
Passo 4
Tá quase acabando, mas antes da gente encontrar as forças de tração, temos que encontrar os ângulos formados em cada tração, para isso é bom lembrarmos que a derivada é a tangente do ângulo formado em relação ao eixo, assim:
Finalmente, as trações: