Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 125
Determine a força normal, a força cortante e o momento fletor interno nos pontos da estrutura.
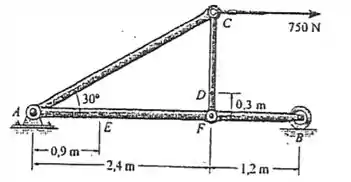
Passo 1
Desejamos encontrar o valor dos esforços internos para os pontos e . Para isso, tomemos o seguinte diagrama de forças
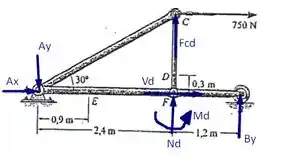
Das equações de equilíbrio podemos fazer
Do membro temos
Passo 2
Analisando a parte mais baixa da estrutura, vamos ter
Resposta
Exercícios de Livros Relacionados
Determine as forças normal e cortante e o momento fletor em uma seção passando pelo ponto C . Considere P=8k N .
Duas vigas estão presas ao membro vertical de modo que as conexões estruturais transmitem as cargas mostradas. Determine as forças normal e cortante e o momento fletor que atuam em uma seção que passa
Determine a distância a como uma fração do comprimento L da viga para localizar o suporte derolete de modo que o momento fletor na viga em B seja zero.
O cabo se romperá quando estiver sujeito a uma tração de 2k N . Determine a maior carga vertical P que a estrutura suportará e calcule as forças normal e cortante e o momento fletor em uma seção que p
A viga tem um peso w por unidade de comprimento. Determine as forças normal e cortante e omomento fletor no ponto C em decorrência de seu peso.