Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 53

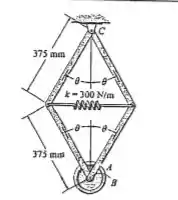
A mola conectada ao mecanismo tem um comprimento livre quando θ = 90 ° . Determine a posição θ para o equilíbrio e investigue a estabilidade do mecanismo nessa situação. O disco A é conectado por pino à estrutura em B e tem um peso de 100 N .

Passo 1

Desejamos encontrar o valor de θ para o equilíbrio e precisamos verificar a estabilidade do mecanismo. Da geometria do problema temos que y = 2 ⋅ 375 ⋅ cos ⁡ θ = 750 ⋅ c o s ⁡ ( θ ) e x = ( 375 - 375 ⋅ sin ⁡ θ ) . Assim, a partir da análise da energia do sistema

U = U E + U G

U = 1 2 ⋅ k x 2 - W ⋅ y =

U =   1 2 ⋅ 300 ⋅ 375 - 375 ⋅ sin ⁡ θ 2 - 100 ⋅ ( 750 ⋅ c o s ⁡ ( θ )   )

Para trabalhar com números mais agradáveis vamos mudar as unidades numéricas que estão em m m para f t . Assim

U =   1 2 ⋅ 16 ⋅ 2 , 5 - 2 , 5 ⋅ sin ⁡ θ 2 - 2 0 ⋅ ( 2,5 ⋅ c o s ⁡ ( θ )   )

Passo 2

O equilíbrio ocorre quando tivermos d V d θ = 0 . Assim,

100 ⋅ sin ⁡ θ ⋅ cos ⁡ θ - 100 ⋅ cos ⁡ θ + 500 ⋅ sin ⁡ θ = 0

Encontramos θ = 37,77 ° ≈ 37,8 ° , para verificarmos a estabilidade vamos substituir esse ponto na segunda derivada e, assim, vamos obter

≈ 125,7 > 0

Portanto, o sistema está em equilíbrio estável quando θ = 37,8 ° .

Resposta

θ = 37,7 8 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se as molas em A e C têm comprimento livre de 250 mm, enquanto a mola em B tem comprimento livre de 300 mm, determine a altura h da plataforma quando o sistema está em equilíbrio. Investigue a estabil
Se a energia potencial para um sistema conservativo com um grau de liberdade é expressa pela relação ( V = 24 sen ⁡ θ + 10 cos ⁡ 2 θ )J , 0 ≤ θ ≤ 90 º º , determine as posições de equilíbrio e investi
A mola está livre quando θ = 45 º ºe tem uma rigidez k = 20k N / m . Determine o ângulo θ para o equilíbrio se cada um dos cilindros pesa 250 N. Despreze o peso dos membros.
Uma mesa de servir uniforme com 5 kg é apoiada em cada lado por pares de ligações idênticas , AB e CD, e molas CE. Se a tigela tem uma massa de 1 kg, determine o ângulo θ onde a mesa está em equilíbri
O cone homogêneo tem uma cavidade cônica cortada, conforme a figura. Determine a profundidade d da cavidade em termos de h de modo que o cone se equilibre sobre o pivô e permaneça em equilíbrio indife