Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 7
Determine a força normal interna, o esforço cortante e o momento nos pontos e da viga simplesmente apoiada. O ponto está localizado à esquerda da força de .
Passo 1
Para determinar o que se pede, deve-se fazer o diagrama de corpo livre da viga para que seja possível determinar alguma reação externa ao apoio da viga. Após isso, deve-se seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas de cada membro seccionado.
Passo 2
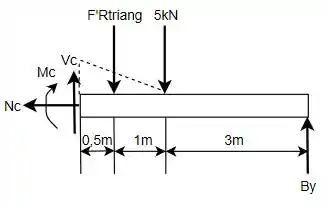
O DCL da viga é dada por:
A carga distribuída exerce uma força resultante sobre a viga em uma determinada posição que devem ser determinados. Como o carregamento é triangular, tem-se que a resultante é dada por:
E a sua posição de atuação será a mesma que a posição do seu centroide para este caso e é dada por:
Passo 3
Agora, tendo apenas as reações indeterminadas é possível determinar a reação em aplicando o somatório de momentos em relação ao ponto e supondo que o momento é positivo no sentido anti-horário, tal que:
Passo 4
Então, pode-se fazer um “corte” no ponto que terá uma de suas seções analisadas.
Logo, fazendo o DCL da seção à direita de e mostrando as forças e reações aplicadas, tem-se que:
Como o comprimento da seção diminuiu, o valor da força resultante gerada pela carga distribuída é alterado. No entanto, como temos o valor da carga apenas na extremidade esquerda, deve-se perceber que a carga é linear e, portanto, o seu valor varia linearmente. Portanto:
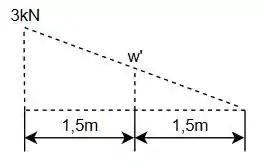
Então:
Com isso, a força resultante gerada pela carga seccionada será:
E o seu ponto de ação será:
Passo 5
Então, voltando ao DCL da seção e aplicando as equações de equilíbrio obtém-se para o eixo :
Para o eixo :
E, aplicando o princípio dos momentos em relação ao ponto e considerando o sentido anti-horário como sendo positivo:
Passo 6
Por fim, fazendo o mesmo processo para o ponto , secciona-se a viga neste ponto e obtém-se o DCL desse membro:
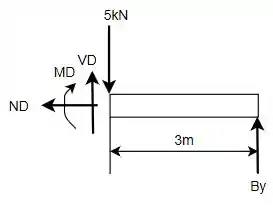
Feito isso, pode-se aplicar as equações de equilíbrio, tal que obtém-se para o eixo :
Para o eixo :
E, aplicando o princípio dos momentos em relação ao ponto e considerando o sentido anti-horário como sendo positivo: