Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 224

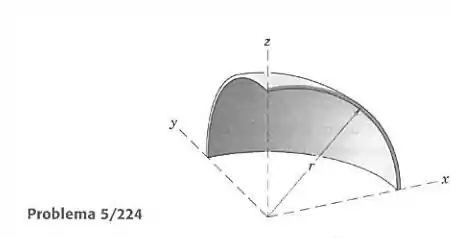
Localize o centro de massa da casca esférica fina, que é formada cortando-se um oitavo de uma casca esférica completa.

Passo 1

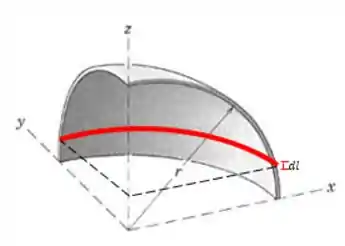
Vamos calcular o centro de massa dividindo a casca em linhas “linhas” de espessura d l que compõem o corpo. Essas linhas serão horizontais, indo da altura z = 0 até a altura z = r , e todas elas têm formato de 1/4 de círculo, começando com raio igual a r no z = 0 até um raio zero no topo. A figura mostra um desses elementos em vermelho:

Passo 2

Olhando perpendicularmente ao plano x z , vamos calcular a coordenada z do centro de massa. As outras coordenadas serão iguais pela simetria. A coordenada z do CM será dada por

z - = ∫ z   d A ∫ d A

Famos fazer nossos cálculos em coordenadas polares, por ser mais fácil se tratando de um formato esférico.

A linha situada num ângulo θ tem um raio r cos ⁡ θ e uma espessura d l = r   d θ . Então sua área d A é dada por:

d A = 1 4 ⋅ 2 π r cos ⁡ θ r   d θ = 1 2 π r 2 cos ⁡ θ d θ

Sua coordenada z é:

z = r sen ⁡ θ

Então nossa integral de cima fica:

∫ z   d A = ∫ 0 π / 2 r sen ⁡ θ ⋅ 1 2 π r 2 cos ⁡ θ d θ = π r 3 2 ∫ 0 π / 2 sen ⁡ θ cos ⁡ θ d θ

Passo 3

Vamos calcular a integral. Como 2 sen ⁡ θ cos ⁡ θ = sen ⁡ 2 θ :

π r 3 2 ∫ 0 π / 2 sen ⁡ θ cos ⁡ θ d θ = π r 3 2 ∫ 0 π / 2 1 2 sen ⁡ 2 θ d θ = - π r 3 8 cos ⁡ 2 θ 0 π / 2 = - π r 3 8 ( cos ⁡ π - cos ⁡ 0 )

= - π r 3 8 - 1 - 1 = π r 3 4

Agora falta a integral de baixo ∫ d A que é a área da casca. A área total de uma esfera é 4 π r 2 , então a área de um oitavo é:

A = ∫ d A = 1 8 ⋅ 4 π r 2 = π r 2 2

Finalmente, dividindo obtemos z - :

z - = ∫ z   d A ∫ d A = π r 3 4 π r 2 2 = π r 3 4 ⋅ 2 π r 2 = r 2

Pela simetria então temos todas as coordenadas:

x - = y - = z - = r 2

Resposta

x - = y - = z - = r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a coordenada z do centro de massa da casca esférica homogênea de raio r correspondente a um quarto de uma esfera.
Determine a coordenada z do centroide do volume obtido pela revolução da área triangular sombreada de 360° em torno do eixo z.
A barra esbelta homogênea tem uma seção transversal uniforme e está dobrada na forma mostrada. Calcule a coordenada y do centro de massa da barra. (Lembrete: O comprimento do arco diferencial é d L =
Localize o centro de massa do corpo sólido homogêneo cujo volume é determinado pela revolução da área sombreada de 360° em torno do eixo z.
Determine a coordenada x do centro de massa da casca cilíndrica de espessura uniforme e pequena.