Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 55

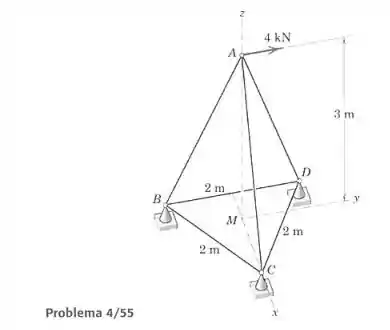
Determine as forças nos elementos A B , A C e A D . O ponto M é o centroide do triângulo B C D .

Passo 1

Como temos três incógnitas, T A B , T A C e T A D , aplicando as três equações de equilíbrio no nó A somos capazes de encontrar as incógnitas. Para isso, precisamos encontrar os vetores unitários que indicam as direções das forças.

Passo 2

Pra achar os vetores unitários vamos primeiro determinar as coordenadas dos pontos, sendo M a origem do sistema de coordenadas. As coordenadas de A são encontradas facilmente:

r → A = 3 k ^

Observamos o plano x y , sabendo que a distância do centroide aos vértices no triângulo equilátero é 2 h / 3 sendo h a altura do triângulo:

d = 2 h 3 = 2 3 ⋅ 3 l 2 = 2 3 ⋅ 3 2 ⋅ 2 = 2 3 3 = 1,555   m

x B = - 1,155 sen ⁡ 30 ° = - 0,578 ; y B = - 1

x D = x B = - 0,578

y D = - y B = 1

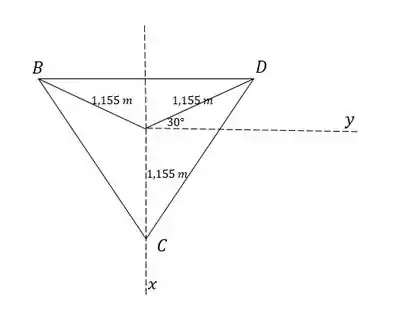
Então:

r → B = - 0,578 i ^ - j ^

r → B = = - 0,578 i ^ + j ^

r → C = 1,155 i ^

Passo 3

Agora vamos encontrar os vetores unitários n ^ A B , n ^ A C e n ^ A D :

r → A B = r → B - r → A = - 0,578 i ^ - j ^ - 3 k ^

Calculando o módulo:

r → A B = 0,578 2 + 1 2 + 3 2 = 3,215

Então:

n ^ A B = - 0,578 i ^ - j ^ - 3 k ^ 3,215 = - 0,18 i ^ - 0,312 j ^ - 0,933 k ^

n ^ A D será o mesmo mas com coordenada y contrária:

n ^ A D = - 0,18 i ^ + 0,312 j ^ - 0,933 k ^

Agora achamos n ^ A C :

r → A C = 1,155 i ^ - 3 k ^

O módulo é o mesmo de r → A B , então:

⇒ n ^ A C = 1,555 i ^ - 3 k ^ 3,215 = 0,359 i ^ - 0,933 k ^

Passo 4

Temos agora as expressões das forças, mas ainda os módulos como incógnita:

T → A B = T A B ( - 0,18 i ^ - 0,312 j ^ - 0,933 k ^ )

T → A C = T A C ( 0,359 i ^ - 0,933 k ^ )

T → A D = T A D ( - 0,18 i ^ + 0,3117 j ^ - 0,933 k ^ )

Agora fazemos as três equações de equilíbrio para A :

∑ F x = 0 ⇒ - 0,18 T A B + 0,359 T A C - 0,18 T A D = 0

Vamos isolar A C para substituir nas próximas equações:

0,359 T A C = 0,18 T A B + 0,18 T A D

⇒ T A C = 0,501 T A B + 0,501 T A D

Passo 5

Agora em z :

∑ F z = 0 ⇒ - 9,333 T A B - 9,333 T A C - 9,333 T A D = 0

Dividindo tudo por 0,933 e substituindo o valor de T A C encontrado anteriormente:

- T A B - T A C - T A D = 0 ⇒ - T A B - 0,501 T A B - 0,501 T A D - T A D = 0

⇒ - 1,501 T A B - 1,501 T A D = 0

Dividindo por 1,501 :

- T A B - T A D = 0 ⇒ T A D = - T A B

A equação para T A C fica:

T A C = 0,501 T A B + 0,501 T A D = 0,501 T A B - 0,501 T A B = 0

Passo 6

Faltou a equação para y . Nessa última temos também a força de 4 kN aplicada em A :

∑ F y = 0 ⇒ - 0,312 T A B + 0,359 T A C + 0,312 T A D + 4 = 0

Substituimos os valores de T A C = 0 e T A D = - T A B :

- 0,312 T A B - 0,312 T A B + 4 = 0 ⇒ 0,624 T A B = 4

Então:

T A B = 6,41   k N

T A D = - 6,41   k N

Resposta

T A B = 6,41   k N

T A C = 0

T A D = - 6,41   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força nos membros D C ,H IeJ I da treliça. Indique se os membros estão sob tração ou compressão.
Determine a força nos membros G F ,G DeC D da treliça. Indique se os membros estão sob tração ou compressão.
Usando o método dos nós, determine a força em cada elemento da treliça mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.
Usando o método dos nós, determine a força em cada elemento da treliça mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.
Usando o método dos nós, determine a força em cada elemento da treliça mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.