Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 17

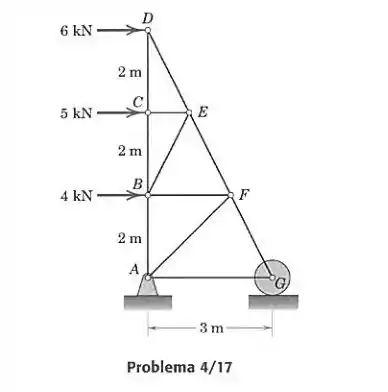
Determine as forças nos elementos A F , B E , B F e C E da treliça carregada.

Passo 1

Primeiro devemos analisar as força externas que atuam na treliça. Temos uma reação vertical em C e uma reação em A , então fazemos as equações de equilíbrio para a treliça como um todo:

∑ F x = 0 ⇒ 6 + 5 + 4 + A x = 0 ⇒ A x = - 15   k N

∑ F y = 0 ⇒ A y + G y = 0

∑ M A = 0 ⇒ - 6 6 - 5 4 - 4 2 + G y 3 = 0 ⇒ 3 G y = 64 ⇒ G y = 64 3   k N

⇒ A y = - 64 3   k N

Passo 2

Vamos resolver as equações de equilíbrio em x e y   para cada nó, começando de cima. As forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração. Primeiro devemos analisar os ângulos importantes da treliça.

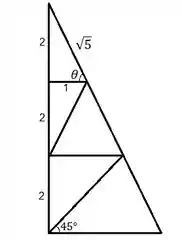
Por semelhança de triângulos obtemos C E - = 1   m . Então por Pitágoras temos:

D E - = 1 2 + 2 2 = 5

Agora já temos sen ⁡ θ e cos ⁡ θ e podemos resolver as equações para os nós.

Passo 3

Nó D:

∑ F x = 0 ⇒ 6 + D E cos ⁡ θ = 0 ⇒ D E = - 6 cos ⁡ θ ⇒ D E = - 6 5   k N   ( C )

∑ F y = 0 ⇒ - C D - D E sen ⁡ θ = 0 ⇒ C D = - 6 5 - 2 5 ⇒ C D = 12   k N   ( T )

Passo 4

Nó C:

∑ F x = 0 ⇒ C E = - 5   k N   ( C )

∑ F y = 0 ⇒ C D - B C = 0 ⇒ B C = 12   k N   ( T )

Passo 5

Nó E:

∑ F x = 0 ⇒ - B E cos ⁡ θ - C E - D E cos ⁡ θ + E F cos ⁡ θ = 0

Substituindo os cossenos:

- B E 5 + 5 + 6 5 5 + E F 5 = 0 ⇒ E F = B E - 11 5  

∑ F y = 0 ⇒ D E sen ⁡ θ - B E sen ⁡ θ - E F sen ⁡ θ = 0

Substituindo os senos e o valor de E F em função de B E :

- 6 5 - B E - B E - 11 5 = 0 ⇒ - 2 B E + 5 5 = 0 ⇒ B E = 5 5 2   k N   ( T )

Passo 6

Nó B:

∑ F x = 0 ⇒ 4 + B E cos ⁡ θ + B F = 0

Substituindo o cosseno e B E , e isolando B F :

B F = - 4 - 5 5 2 ⋅ 1 5 ⇒ B F = - 13 2   k N   ( C )

∑ F y = 0 ⇒ B C + B E sen ⁡ θ - A B = 0

Isolando A B e substituindo o seno, B C e B E :

A B = 12 + 5 5 2 ⋅ 2 5 ⇒ A B = 17   k N

Passo 7

Nó A:

∑ F y = 0 ⇒ A B + A F sen ⁡ 45 ° + A y = 0 ⇒ 17 + 2 2 A F - 64 3 = 0 ⇒ 2 2 A F = 13 3

⇒ A F = 13 2 3   k N   ( T )

Resposta

A F = 13 2 3   k N = 6,13   k N   ( T )

B E = 5 5 2   k N = 5,59   k N   ( T )

B F = 6,50   k N   ( C )

C E = 5,00   k N   ( C )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força nos membros E F ,C FeB C da treliça. Diga se os membros estão sob tração ou compressão.
46. Determine a força nos elementos D G e E G na treliça mostrada na figura.
45. Determine à força nos elementos B D e D E na treliça mostrada na figura.
48. Uma treliça de piso é carregada tal como mostra a figura. Determine a força nos elementos F I ,H I e H J .
47. Uma treliça de piso é carregada tal como mostra a figura. Determine a força nos elementos C F ,E F e E G .