Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 32
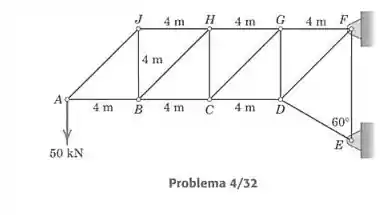
Determine as forças nos elementos e para a treliça carregada e apoiada como mostrado. A indeterminação estática dos apoios afeta o seu cálculo?
Passo 1
Vamos calcular as forças pelo método das seções. Traçamos uma seção passando por , e , tratando a parte da esquerda como se fosse um só corpo rígido. A indeterminação estática ocorre do lado direito, no elemento , então nosso cálculo não é afetado. O nosso desenho então fica assim:
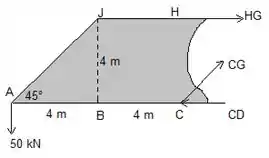
Devemos resolver as equações de equilíbrio pra esse corpo pra encontrarmos as forças de e .
Passo 2
Resolvendo a equação da soma de forças no eixo podemos encontrar a força :
O sinal positivo indica que acertamos o sentido da força no desenho. Agora podemos igualar a zero o momento em torno de , já que a força desconhecida não entra no cálculo:
O sinal positivo indica que o elemento está de fato tracionado como indicamos no desenho.