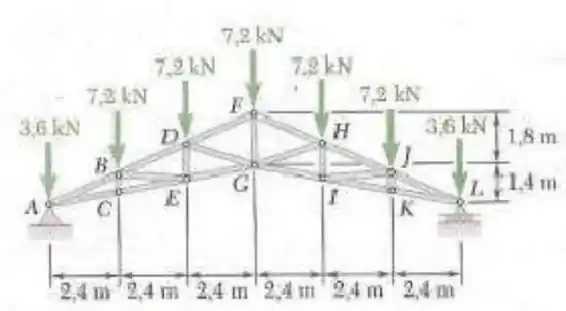
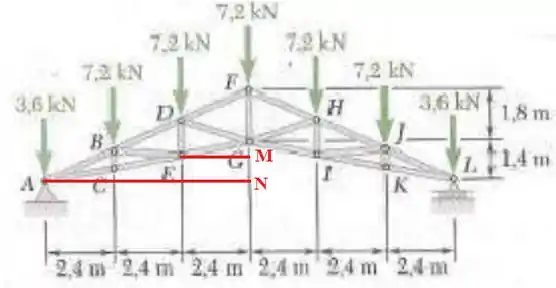
6.51. Uma treliça de telhado Howe em forma de tesoura é carregada tal como mostra a figura. Determine a força nos elementos DF, DG e EG.
Passo 1
Vamos fazer o desenho disso
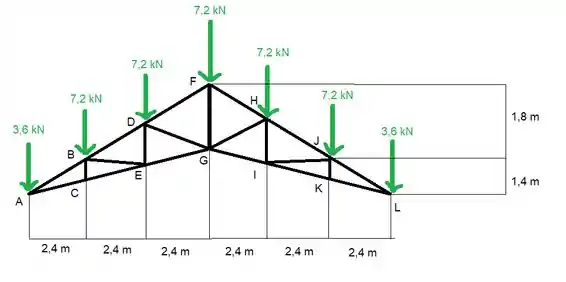
O que a gente consegue tirar só da imagem são as forças de reação nas pontas
E
Passo 2
O melhor que a gente pode fazer aqui é usar o método das seções, vamos seccionar desse jeito
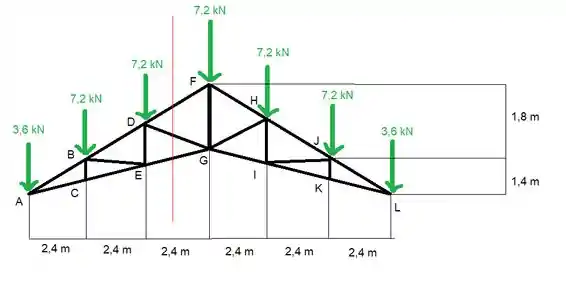
E aí a gente tem
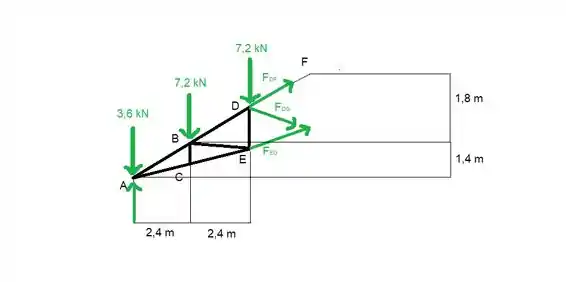
Só vamos mudar um pouquinho o vetor de lugar para facilitar as contas
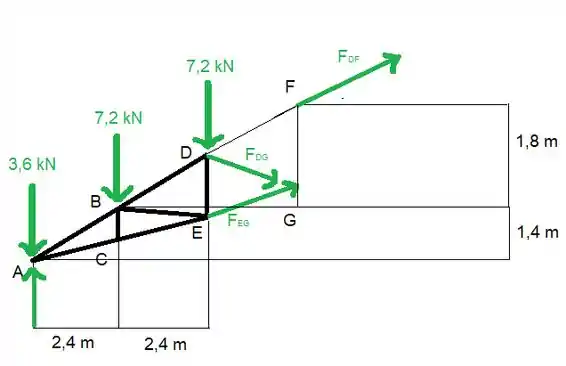
Passo 3
Beleza, agora a gente pode calcular os momentos, vamos usar o momento no ponto G. Repare que as forças , são forças que agem no ponto G, então elas não são consideradas no momento.
Sendo que θ é o ângulo que a direção AF faz com a horizontal.
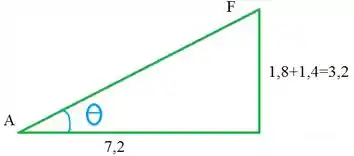
Vamos usar esse triângulo para ajudar
Vamos precisar calcular a hipotenusa desse triângulo
Agora a gente pode encontrar já que é a única incógnita na equação.
Agora a gente pode calcular o momento no ponto A, repare antes que as forças e não produzem nenhum efeito de rotação se estivermos analisando o ponto A, portanto são forças desprezíveis no cálculo do momento.
Vamos decompor ! Mas falta uma coisa ainda: um dos catetos está faltando. Então a gente tem que determinar a distância em y da reta , para isso a gente isso a gente usa a propriedade dos triângulos semelhantes. Traçando retas horizontais pelos pontos A e D, formamos 2 triângulos semelhantes. E assim podemos achar a altura h mostrada no desenho.
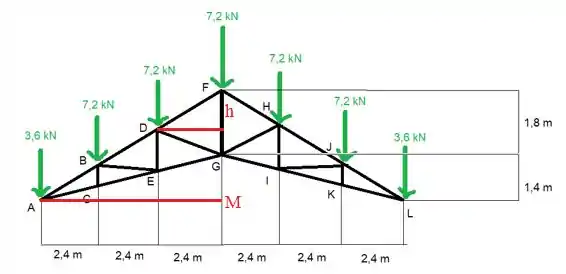
Assim a distância vertical da reta GD será:
Agora a gente pode finalmente decompor
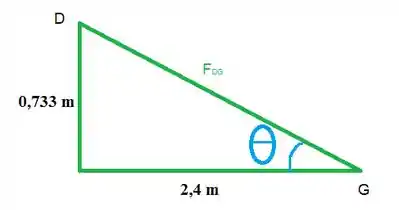
Ainda precisamos calcular a hipotenusa, :/
Agora a gente isola
Agora para determinar vamos usar o momento em D
Agora precisamos decompor a força e encontrar a distância vertical da barra EG. Se traçarmos 2 horizontais, partindo dos pontos A e E, criamos 2 triângulos semelhantes. E a altura GM é igual a distância vertical da barra EG.
Pela semelhança de triângulos:
Do triângulo EGM, achamos o comprimento da barra EG:
Então, decompondo :
Assim,