Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 79

79- A conexão uniforme O A tem uma massa de 20   k g e está apoiada no plano vertical pela mola A B cujo comprimento é de 400   m m quando não está esticada. Faça um gráfico da energia potencial total V e da sua derivada d V / d θ em função de θ , de θ = 0 até θ = 120 . A partir dos gráficos, identifique os valores de equilíbrio de θ e a correspondente estabilidade do equilíbrio. Considere V g = 0 em um nível passando por O .

Passo 1

Para calcular a energia potencial gravitacional do sistema devemos traçar a linha de energia potencial nula que passa em O , logo quando a barra roda θ o centro de massa fica embaixo dessa linha e sua altura em função de θ será do mesmo tamanho da reta roxa h . Logo

cos ⁡ θ = - h 0.2 → h = - 0.2 cos ⁡ θ

Onde 0.2   é 200   m m convertido para metros.

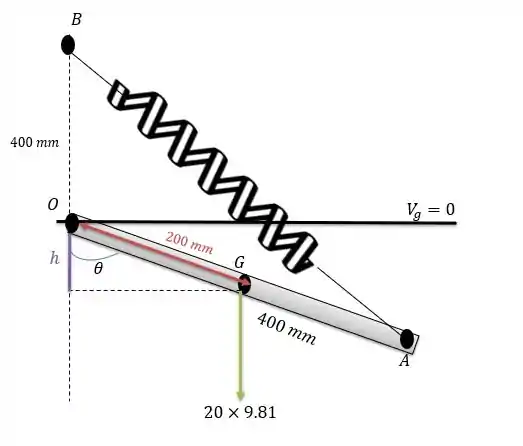
Logo a energia potencial gravitacional do sistema será:

V g = m g h = 20 × 9.81 × ( - 0.2 cos ⁡ θ ) = - 39.24 cos ⁡ θ

Passo 2

Para encontrar a energia potencial elástica nós temos que saber que seu comprimento natural l 0 é de 400 m m = 0.4   m logo seu alongamento vai ser dado por:

Δ x = l f - l 0

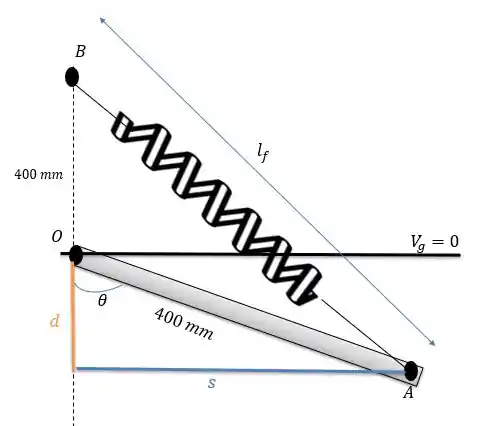
Para calcular o valor do alongamento da mola precisamos antes saber os valores de d e de s que são obtidas utilizando trigonometria básica.

sin ⁡ θ = s 0.4 → s = 0.4 sin ⁡ θ

cos ⁡ θ = d 0.4 → d = 0.4 cos ⁡ θ

Agora podemos achar o valor de l f fazendo Pitágoras no triângulo retângulo grandão.

l f 2 = ( 0.4 + 0.4 cos ⁡ θ ) 2 + ( 0.4 sin ⁡ θ ) 2

l f 2 = 0.4 2 ( 1 + cos ⁡ θ ) 2 + 0.4 2 sin 2 ⁡ θ

l f 2 = 0.4 2 [ 1 + 2 cos ⁡ θ + cos 2 ⁡ θ + sin 2 ⁡ θ ] = 2 × 0.4 2 1 + c o s θ

Da fórmula do arco metade temos que:

cos ⁡ θ 2 = 1 + cos ⁡ θ 2 → 1 + cos ⁡ θ = 2 × sin 2 ⁡ θ 2

Logo:

l f 2 = 4 × 0.4 2 × cos 2 ⁡ θ 2

Então o comprimento final da mola será:

l f = 2 × 0.4 × cos ⁡ θ 2 = 0.8 cos ⁡ θ 2

Então a variação do comprimento da mola será:

Δ x = 0.8 cos ⁡ θ 2 - 0.4 = 0.4 2 cos ⁡ θ 2 - 1

Finalmente podemos escrever a energia potencial elástica do sistema que será:

V e = 1 2 k Δ x 2 = 550 2 0.4 2 2 cos ⁡ θ 2 - 1 2 = 44 2 cos ⁡ θ 2 - 1 2

Passo 3

Logo a energia total do sistema será:

V = 44 2 cos ⁡ θ 2 - 1 2 - 39.24 cos ⁡ θ

E sua derivada em relação a θ será:

d V d θ = 88 2 cos ⁡ θ 2 - 1 × - sin ⁡ θ 2 + 39.24 sin ⁡ θ

Como sin ⁡ 2 θ = 2 sin ⁡ θ cos ⁡ θ   logo:

d V d θ = 88 - sin ⁡ θ + sin ⁡ θ 2 + 39.24 sin ⁡ θ

Plotando os dois gráficos em software nós encontramos a seguinte resposta.

Onde V está representada em verde e d V / d θ em azul e com isso dois pontos de equilíbrio, em θ = 0 e θ = 51.055 ° .

Pelo gráfico fica um pouco difícil dizer a concavidade para θ nessas posições, então vamos fazer a segunda derivada para poder calcular a estabilidade.

d 2 V d θ 2 = 88 - cos ⁡ θ + cos ⁡ θ 2 2 + 39.24 cos ⁡ θ

E com essa expressão temos as seguintes condições:

d 2 V ( 0 ) d θ 2 = 88 - cos ⁡ 0 + cos ⁡ 0 2 + 39.24 cos ⁡ 0 = - 4.76 → i n s t á v e l

d 2 V ( 51.055 ) d θ 2 = 88 - cos ⁡ 51.055 + cos ⁡ 51.055 2 2 + 39.24 × cos ⁡ 51.055 = 9.055

O que configura numa posição estável.

Resposta

θ = 0 → i n s t á v e l

θ = 51.055 → e s t á v e l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mecanismo está sujeito a uma força P = 2 kN. Determine o ângulo θ para o equilíbrio. A mola está livre quando θ = 0 ° . Despreze a massa dos membros.
Determine a intensidade exigida da força P para manter o equilíbrio do mecanismo em θ = 60 ° . Cada membro tem uma massa de 20 kg.
A ponte de 2 Mg, com centro de massa no ponto G, é levantada pelas duas vigas CD, localizadas em cada lado da ponte. Se o contrapeso E de 2 Mg estiver conectado às vigas como mostrado, determine o âng
O mecanismo conectado por pinos é restringido por um pino em A e um rolete em B. Determine a força P que deve ser aplicada ao rolete para manter o mecanismo em equilíbrio quando θ = 30 º º. A mola est
5. Determine o ângulo θ onde a barra de 50k g está em equilíbrio. A mola está livre em θ = 60 ° .