Determine as forças nos elementos , e da treliça simétrica carregada.

Agora vamos tentar encontrar a força em usando o método das seções:

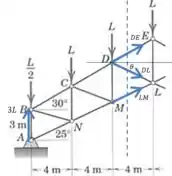
E vamos calcular o momento em relação ao ponto , para que as forças e tenham momento nulo:

Além das força com múltiplos de , cujas distâncias até o ponto estão bem claras pelo desenho, temos a componente da força agindo à seguinte distância:

Que em temos das alturas é simplesmente o seguinte: . E então ficamos com a seguinte expressão para o momento:

E o sinal negativo indica que essa é uma força de compressão.

Agora vamos usar as equações de equilíbrio das forças em cada direção, ainda olhada para a mesma seção da treliça.

Vamos precisar encontrar o ângulo para poder projetar as forças nos eixos:

E agora já podemos escrever as equações de equilíbrio em cada eixo:

E organizando um pouco:

E podemos resolver esse sistema multiplicando a primeira linha por e a segunda por e então somando as duas equações:

E então substituindo em qualquer uma das equações vamos encontrar:

E então fica faltando apenas encontrar a força . Com as informações que temos agora,podemos simplesmente considerar uma equação de equilíbrio para o ponto :

E por simetria sabemos que , ou seja:

Que é uma força de tração.