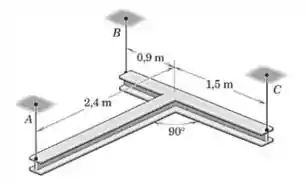
Duass vigas em I de aço, cada uma com uma massa de , estão soldadas em um ângulo reto e sustentadas por cabos verticais de forma que as vigas se mantêm em um plano horizontal. Calcule a força trativa em cada um dos cabos , e .
Passo 1
Primeiro precisamos representar os eixos e as forças no desenho:
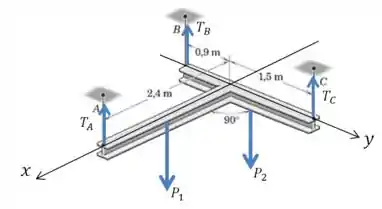
Para que esse sistema esteja em equilíbrio, sabemos que os torques resultantes em relação aos dois eixos têm que ser nulos!
Perceba que os pesos atuam nos pontos médios de cada viga. está a da origem, e está a .
Passo 2
Primeiro vamos escrever uma expressão para o torque em relação ao eixo . Todas as forças que têm uma linha de ação cruzando esse eixo vão ser anuladas:
Deixamos com sinal negativo as forças que favorecem a rotação no sentido horário.
Agora vamos fazer o mesmo para o momento em relação ao eixo :
Podemos organizar essas duas equações em um sistema:
E como as duas vigas têm a mesma massa podemos substituir .
Beleza, mas ainda temos três variáveis desconhecidas , e ) e só duas equações: precisamos achar outra equação para poder resolver o sistema completamente!
Passo 3
Vamos usar a condição de equilíbrio para as forças:
Agora sim, temos um sistema completo:
Pela segunda equação podemos encontrar :
Agora vamos substituir isso na terceira equação:
E agora podemos substituir na primeira equação:
E então é:
Resposta
As forças são , e .