Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 4

7.4. Determine as forças internas no ponto J quando α = 0 °

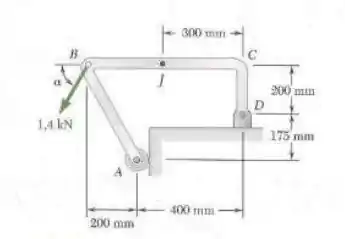
Passo 1

Vamos começar desenhando a situação

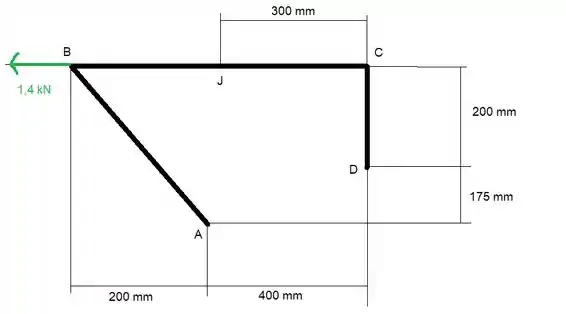
Só com isso já podemos determinar as forças de reação em D. Só precisamos usar as equações de equilíbrio

∑ F y = 0

Só tem uma força agindo em y, logo

D y = 0

Agora vamos usar o momento no ponto A

∑ M A = 0

1,4 ⋅ 0,375 - D x ⋅ 0,175 = 0

Logo

D x = 3   k N

Passo 2

Agora para achar as forças que precisamos a gente tem que usar o corpo livre em J C D -

Onde F é a força axial, V é o esforço cortante e M o momento fletor.

Agora é só usar as equações de equilíbrio

∑ F x = 0

3 - F = 0

Logo

F = 3   k N

∑ F y = 0

- V = 0

Logo

V = 0

E finalmente

∑ M j = 0

3 ⋅ 0,2 - M = 0

Logo

M = 0,6   k N ⋅ m

Resposta

F = 3   k N

V = 0

M = 0,6   k N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O macaco A B é usado para acertar a viga fletida D E usando a montagem mostrada. Se a força compressiva axial no macaco é de 25k N , determine o momento interno desenvolvido no ponto C da viga superio
Determine as componentes x , y e z da carga interna em uma seção passando pelo ponto C na tubulação. Despreze o peso da tubulação. Faça F 1 = 350 j - 40 0 kk N e F 2 = 15 0 i - 300 kk N .
Determine a força normal interna, o esforço cortante e o momento nos pontos F e G da viga composta. O ponto F está localizado à direita da força 2,5k N , enquanto o ponto G está localizado à direita d
A lança do guindaste suporta uma carga de 3,75k N através do carrinho que desliza por cima da lança. Determine a força normal interna, o esforço cortante e o momento no ponto C da lança quando o carri
Determine a força normal interna, o esforço cortante e o momento que atuam no ponto C . A unidade de resfriamento tem uma massa total de 225k g com centro de massa em G .