Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 16

7.16. Sabendo que o raio de cada roldana é 150 mm, que α = 3 0 ° e desprezando o atrito, determine as forças internas em (a) no ponto J, (b) no ponto K

Passo 1

Vamos começar desenhando a situação

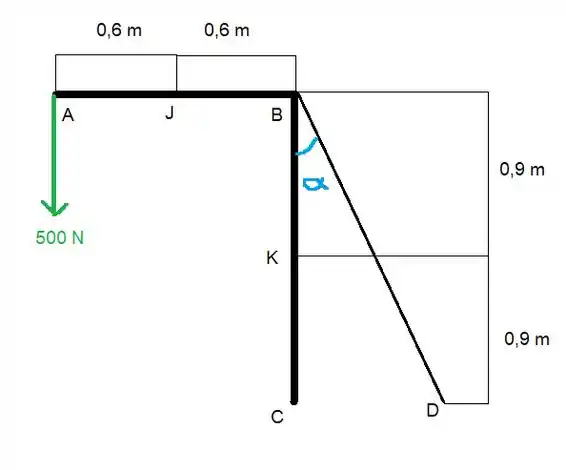
Bem, a gente consegue ver que a tensão no cabo é de 500   N .

Passo 2

Agora para achar as forças que precisamos para resolver o item (a) a gente tem que usar o corpo livre em A J - , lembrando que a tensão no cabo é de 500   N

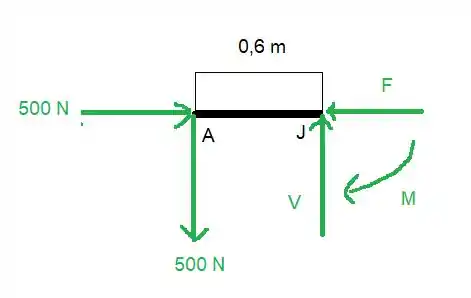
Agora vamos usar as equações de equilíbrio

∑ F x = 0

500 - F = 0

Então

F = 500   N

Agora para y

∑ F y = 0

V - 500 = 0

Logo

V = 500   N

E agora finalmente o momento em J

∑ M J = 0

500 ⋅ 0,6 - M = 0

Logo

M = 300   N ⋅ m

Passo 3

Agora para fazer o item (b), precisamos fazer o corpo livre para A B K -

Agora vamos usar as equações de equilíbrio

∑ F x = 0

500 - 500 + 500 sin ⁡ 3 0 ° - V = 0

Logo

V = 250   N

Agora em y

∑ F y = 0

- 500 - 500 cos ⁡ 3 0 ° + F = 0

Logo

F = 9 33   N

Agora finalmente vamos usar o momento no ponto K

∑ M k = 0

500 ⋅ 1,2 - 500 sin ⁡ 3 0 ° ⋅ 0,9 - M = 0

Logo

M = 375   N ⋅ m

Resposta

(a)

F = 500   N

V = 500   N

M = 300   N ⋅ m

(b)

V = 250   N

F = 9 33   N

M = 375   N ⋅ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6.119. Determine as componentes horizontal e vertical da reação que os pinos exercem sobre o membro ABC.
6.120. Determine o momento de binário M que precisa ser aplicado no membro DC para o equilíbrio do mecanismo de retorno rápido. Expresse o resultado em função dos ângulos ϕeθ , da dimensão L e da forç
6.114. A pá do trator transporta uma carga de 500k g de terra, com centro de massa em G. Calcule as forças desenvolvidas nos cilindros hidráulicos IJ e BC devido a essa carga.
6.116. Se a força de prensagem horizontal que o grampo exerce sobre o bloco liso de madeira em E é N E = 200N , determine a força P aplicada no cabo do grampo articulado.
6.113. Mostre que o peso W 1 do contrapeso em H necessário para o equilíbrio é W 1 = b a ⋅ W e portanto, ele é independente da posição da carga W na plataforma.