Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.7 - Ex. 145

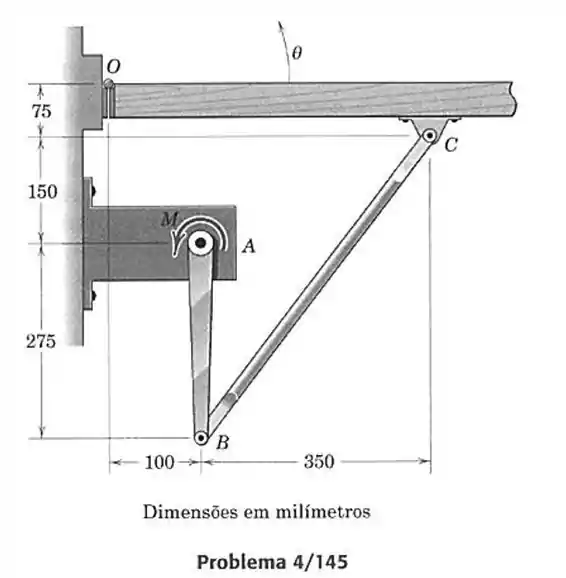
145- Um dispositivo de abertura de porta é mostrado na figura. As dobradiças com molas em O fornecem um momento K T θ que tende a fechar a porta, onde θ é o ângulo de abertura da porta e a constante de torção da mola é K T = 56.5   N m / r a d . O motor em A fornece um momento variável M de forma que a porta que se abre lentamente está sempre em equilíbrio quase-estático. Determine para a faixa 0 ≤ θ ≤ 90 , o momento M e a força no pino B em função de θ . Calcule o valor de M para θ = 45 .

Passo 1

Vamos fazer o desenho desse dispositivo com o ângulo θ no eixo O C , sabendo que A B gira no sentido anti-horário .

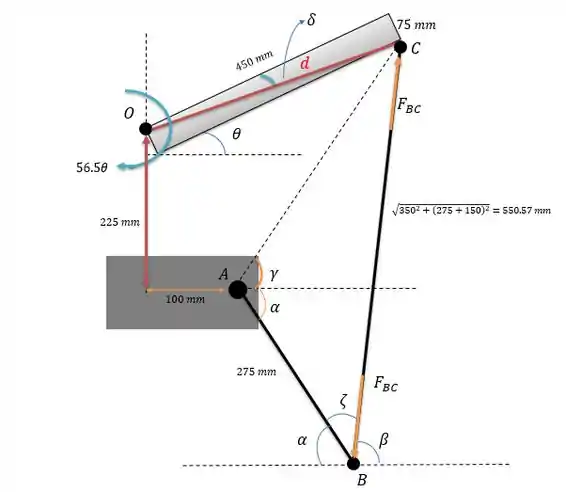
Vamos precisar da distância d igual a O C pois ela vai ser onde a força F B C vai fazer momento em O e assim poder correlacionar ela com o momento M .

d = 0.45 2 + 0.075 2 = 0.456  

δ = t g - 1 75 450 = 9.46   °

Vamos descobrir agora todas as distâncias presentes no dispositivo, tal como A C onde tem que se rebater a barra com pivô em O na horizontal e na vertical

A C = 0.450 cos ⁡ θ + 0.075 sin ⁡ θ - 0.1 2 + ( 0.225 + 0.45 sin ⁡ θ - 0.075 cos ⁡ θ ) 2

Agora pela lei dos cossenos conseguimos encontrar os ângulos:

γ + α = cos - 1 ⁡ A B 2 + A C 2 - B C 2 2 × A B × A C = cos - 1 ⁡ A C 2 - 0.227 0.55 A C

Onde γ é a tangente do mesmo triângulo retângulo formado pela hipotenusa A C :

γ = t g - 1 0.225 + 0.45 sin ⁡ θ - 0.075 cos ⁡ θ 0.45 cos ⁡ θ + 0.075 sin ⁡ θ - 0.1

Logo α será:

α = cos - 1 ⁡ A C 2 - 0.227 0.55 A C - t g - 1 0.225 + 0.45 sin ⁡ θ - 0.075 cos ⁡ θ 0.45 cos ⁡ θ + 0.075 sin ⁡ θ - 0.1

Agora pela lei dos cossenos vamos encontrar ζ :

ζ = cos - 1 ⁡ A B 2 + B C 2 - A C 2 2 × A B × B C = cos - 1 ⁡ 0.379 - A C 2 0.303

Logo o valor de β será:

α + ζ + β = 180

β = 180 - α - ζ

Passo 2

Agora podemos analisar a somatória dos momentos em O e assim encontrar uma relação para a força intermediária F B C :

∑ M O = 0

56.5 θ - F B C × d sin ⁡ β - θ + δ = 0

F B C = 56.5 θ 0.456 sin ⁡ β - θ + δ

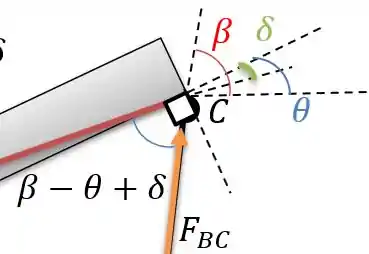
Passo 3

Agora podemos fazer a somatória dos momentos em A , para isso vamos espelhar a a distância 0.275 para ser paralela a força

M = 0.275 F B C sin ⁡ ζ

Plotando tudo em ordem encontramos os seguintes gráficos para M   e F B C :

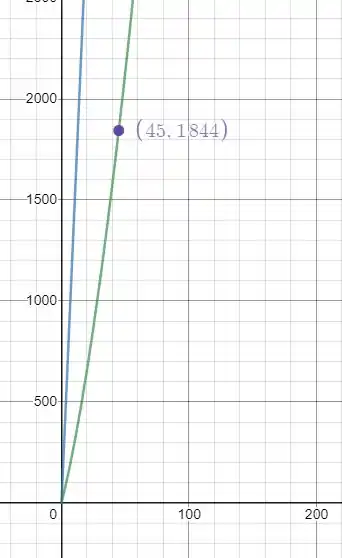
Onde a curva verde é o gráfico verde é o gráfico de M e o azul o de F B C .

Link: https://www.desmos.com/calculator/yd08kgsdbs

Resposta

e m   θ = 45 ; M = 1844   N m

Quem achar o erro ganha um biscoito

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força de corte F exercida na haste S em termos das forças P aplicadas nos cabos da fresa de alta resistência.
Calcule a magnitude da força que atua no pino em D . O pino C é fixado em D E e encosta na fenda lisa na placa triangular.
Determine os componentes de todas as forças que atuam em cada membro da estrutura carregada.
No grampo de mola mostrado, uma mola interna é enrolada em torno do pino em A e as extremidades da mola se apoiam nas superfícies internas das metades do cabo para fornecer a força de aperto desejada.
O dispositivo mostrado na figura é projetado para cravar colchetes em material de moldura de imagem. Para uma força de preensão de 10l b nas alças, determine a força F exercida no colchete.