144- A lança do grande guindaste a beira mar pode girar em torno do elemento vertical . Determine as forças nos elementos e e faça seus gráficos em função do ângulo . A massa da carga é de . O ângulo de elevação de da lança permanece constante; os cabos para controle do ângulo de elevação da lança foram omitidos para maior clareza.
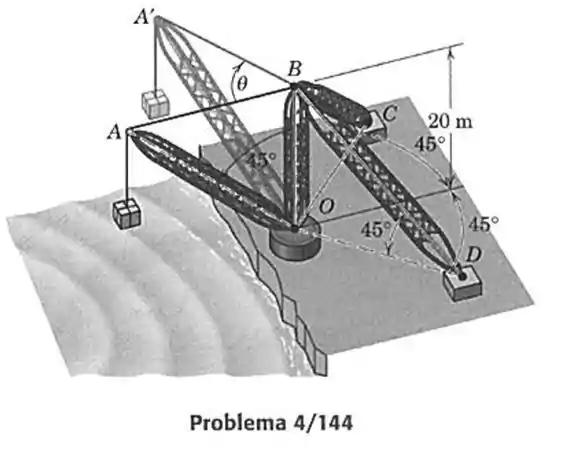
Passo 1
O diagrama de forças desse guindaste pode ser desenhado da seguinte forma.
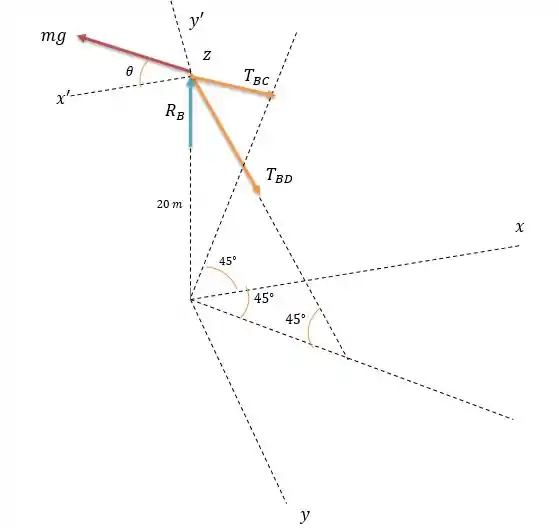
Passo 2
Para resolver esse exercício precisamos resolver a somatória das forças no eixo e a somatória das forças em . Para isso precisamos encontrar a direção do vetor e .
Para isso precisamos descobrir a posição do ponto geométrica e a posição geométrica do ponto .
A distância da reta vale uma vez que o triângulo retângulo é isósceles, assim como o triângulo , e se espelharmos esses valores nos eixos e nós encontraremos os seguintes valores de pontos.
Pois basta fazer o seno e o cosseno de 45 para encontrar esses valores nos eixos.
Agora podemos encontrar a direção dos vetores e .
Começando por .
Para a única diferença é que encontra-se com negativo (refletido). Isso nos dará uma direção de vetor igual a:
Passo 3
Agora podemos fazer a somatória das forças. Fazendo a de bastar multiplicar a direção de do vetor que encontramos e multiplicar com a intensidade da força da seguinte forma:
Agora a somatória das forças em :
Somando as duas equações encontraremos:
Se diminuirmos as duas equações encontraremos:
Como a massa é de temos:
Passo 4
Plotando as duas forças no intervalo de indo de a temos o seguinte comportamento:
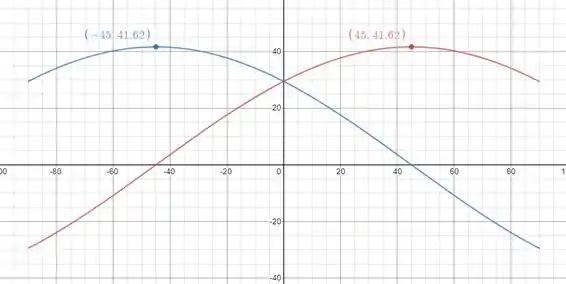
Valores em
A curva azul equivale a e a vermelha a .