Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 6.Problemas - Ex. 15
Determine a força em cada membro da treliça em função da carga e indique se os membros estão sob tração ou compressão.
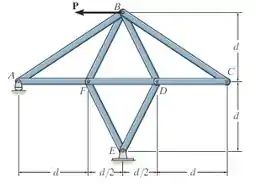
Passo 1
Vamos desenhar o diagrama de corpo livre dessa treliça!
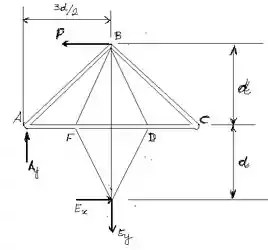
Passo 2
Para todo corpo em equilíbrio, o somatório dos momentos em relação a um ponto deve ser igual a zero. Então, vamos calcular o momento em relação ao ponto . Adotando como sentido positivo o anti-horário, temos:
Além dos momentos, o somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. Assim, adotando como referências positiva as direções para cima e para direita, temos:
Passo 3
Da teoria de treliças, nós temos a ideia dos membros de força zero, que são aqueles que não suportam carregamento algum. Esses membros de força zero são utilizados para aumentar a estabilidade da treliça durante a construção e para fornecer apoio adicional se o carregamento for alterado. No nosso caso, no ponto nós temos que os membros e são membros de força zero. Logo,
Passo 4
Vamos agora analisar o ponto . O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero.
Adotando como referências positivas as direções para direita e para cima, temos:
Passo 5
Vamos agora analisar o ponto . O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero.
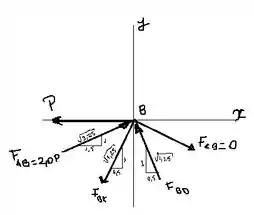
O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. Adotando como referência positiva as direções para direita e para cima, temos:
Temos um sistema de duas equações com duas incógnitas! Vamos resolver para encontrar e .
Passo 6
Vamos agora analisar o ponto . O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero.
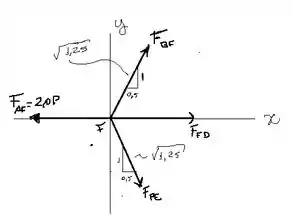
O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. Adotando como referência positiva as direções para direita e para cima, temos:
Passo 7
Vamos agora analisar o ponto . O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero.
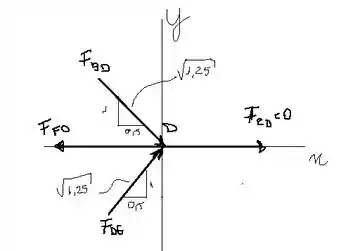
O somatório das forças nos eixos de referência (, para um corpo em equilíbrio, deve ser igual a zero. Adotando como referência positiva as direções para direita e para cima, temos: