Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 81
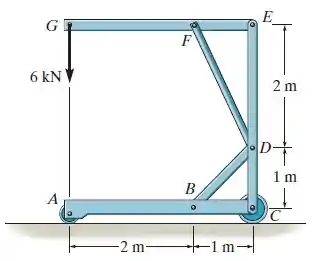
Determine as forças nos membros e da estrutura. Além disso, encontre as componentes horizontal e vertical da reação que o pino em exerce sobre o membro e o membro .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Devemos determinar a força nos membros e e depois as componentes vertical e horizontal no pino em
Como vocês podem observar na questão, a nossa estrutura é composta por várias barras. A ideia para resolvermos a questão é dividir para conquistar.
Então, vamos dividir a estrutura em três partes: a barra , a barra e a barra . Somente fazendo esta divisão vamos conseguir resolver a nossa questão, visto a série de incógnitas (vários vínculos).
Bom, para resolver a questão será necessário esboçar o diagrama de equilíbrio apenas para as barras e . Só devemos tomar muito cuidado ao colocarmos forças que aparecem em dois componentes! Pela lei de ação e reação, elas terão um sentido oposto!
Sendo assim, para a barra , temos:
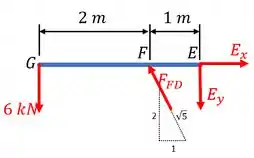
Já para a barra , temos:
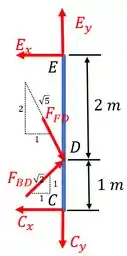
Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
Vamos começar a nossa questão trabalhando com a barra (a única que conhecemos algum valor de força).
Para determinarmos as reações nos apoios, temos que utilizar as relações de equilíbrio (somatório de forças e momentos iguais a zero).
Então, utilizando essas relações, temos:
Resolvendo o sistema acima, obtemos:
E assim descobrimos a nossa primeira incógnita!
Passo 3
Agora temos que repetir todo o procedimento anterior, só que para a barra . Portanto, aplicando as equações de equilíbrio, temos:
Resolvendo o sistema acima, obtemos:
E assim finalizamos a questão!