Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 14
Determine as forças normal e cortante e o momento fletor no ponto da viga.
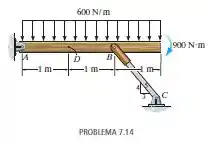
Passo 1
Inhaiiii... beleza???
Nessa questão vamos precisar dos conceitos de estática de praxe:
- Somatório das forças em é igual a zero:
- Em :
- e o momento também:
E bora já começar fazendo o diagrama de corpo livre:
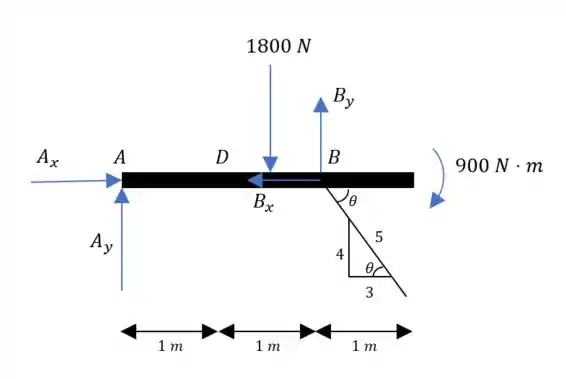
Lembrando que essa carga distribuída podemos substituir por uma pontual bem na metade:
Passo 2
Fazendo do somatório das forças em :
E em :
Para o momento:
E, assim, temos a reação de apoio vertical em :
Ahhhh... Repara bem que podemos relacionar e , né? (aquele triângulo maroto ali não foi dado à toa)
E a reação horizontal em :
Passo 3
Fazendo o corte em:
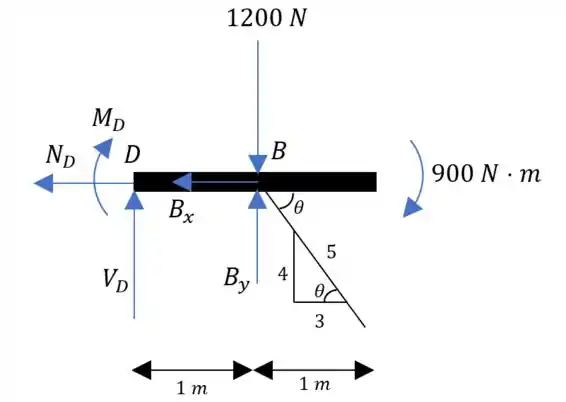
Fazendo o somatório das forças em :
Em :
Para o momento:
Ohhh... acabamos mais uma, heim!? Bora pra próxima, então...
Resposta
Exercícios de Livros Relacionados
Determine a força normal, a força cortante e o momento fletor interno nos pontos D e E da estrutura.
Determine a distância a entre os apoios em termos do comprimento L da viga de modo que o momento na viga simétrica seja zero no centro da viga.
Determine a força normal, a força cortante e o momento fletor interno nos pontos B e C da viga.
Os segmentos de cabo suportam a carga mostrada. Determine a intensidade da força horizontal P de modo que x B = 1,8m .
Os segmentos de cabo suportam a carga mostrada. Determine a distância horizontal x B a partir da força B até o ponto A . Faça P = 200N .