Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 12
Determine a distância a entre os mancais em termos do comprimento do eixo, de modo que o momento fletor no eixo simétrico seja zero em seu centro.
Passo 1
Falaaa galerinha. Tudo bão?
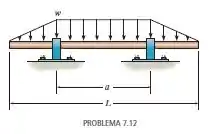
Já vamos começar essa questão montando o bom e velho diagrama de corpo livre:
Repara que dividimos a carga distribuída em três partes e substituímos por cargas pontuais equivalentes.
Vale também lembrar que a carga distribuída referente ao retângulo vai ser situada bem no meio, maaas a do triângulo fica a 1/3 e NÃO na metade, beleza??
- Primeiro triângulo: (lembra que a área do triângulo é base vezes a altura divido por 2? =X)
- Retângulo de base :
- Segundo triângulo:
Ahhh... vamos precisar dos conceitos de estática em que o somatório das forças em é igual a zero:
E dos momentos também é zero:
Passo 2
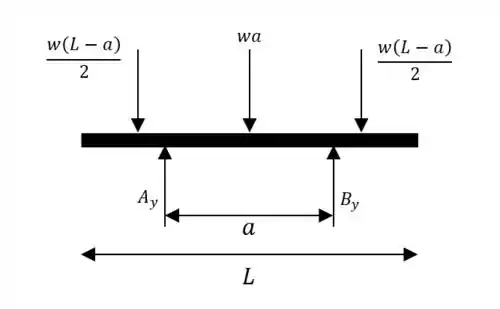
Pra achar as reações de apoio fazemos o somatório das forças em
Pela simetria do problema:
Então:
Passo 3
Agoooora sim vamos começar a questão...
Vamos fazer um corte bem no meio da figura já que o enunciado quer que o momento fletor no eixo simétrico seja igual a zero no seu centro:
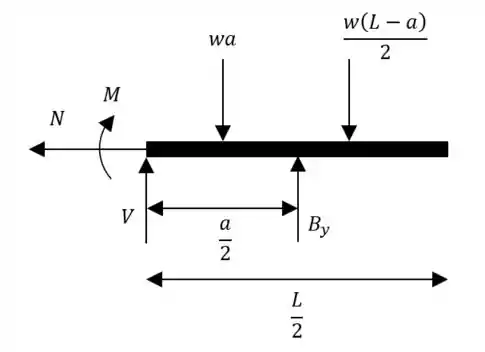
Atençãozinha porque, como cortamos a barra, vamos precisar calcular a carga pontual equivalente a esse pedaço, de novo, heim? E ainda por cima vai mudar de lugar...
Para não precisarmos calcular essa força cortante , vamos fazer o balanço de momento referente a esse ponto:
Que tenhamos forças pra resolver esse algebrismo todo =////
Mas bora lá...
Uma notícia “boa” é que o momento é igual a zero (ok que não fez muita diferença rs).
Resolvendo essa equação do segundo grau:
Como estamos falando de distância... podemos desconsiderar o negativo:
Essa foi, heim?? Vamos pra mais uma??