Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 11
Determine as forças normal e cortante e o momento fletor nos pontos e da viga.
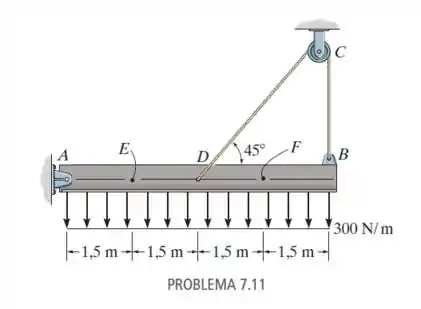
Passo 1
Falaaa... belezinha???
Vamos começar montando o diagrama de corpo livre:
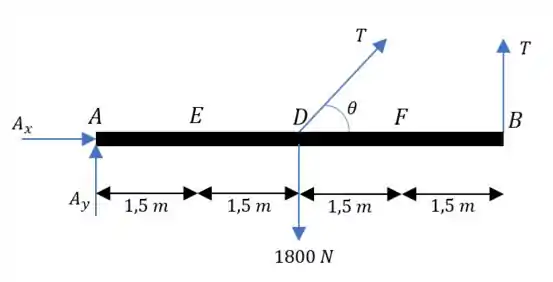
Lembrando que essa carga distribuída pode ser substituída por uma pontual equivalente:
E temos que lembrar que em estática o somatório de forças é igual a zero, tanto em quando em :
Também o somatório dos momentos é igual a zero:
Passo 2
Pra gente não fazer um monte de contas à toa, repara que queremos as forças normal e cortas e o momento fletor SOMENTE nos pontos e .
Daí vamos precisar fazer cortes na barra nesses pontos, então não precisamos achar as reações no ponto , sacou?
Queremos achar essa bendita tração , maaas pra isso fazemos o balanço de momento no ponto :
Passo 3
Fazendo o corte em ficamos com o segmento :
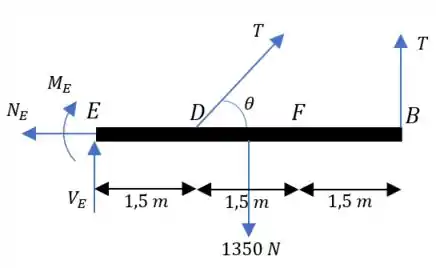
MUUUITA atenção porque agora a carga pontual que substitui a carga distribuída mudou de lugar e de valor, também, ok??? (porque a gente cortou um pedaço, né?)
Fazendo o somatório das forças em podemos encontrar a força normal:
E o somatório das forças em para encontrar a força cortante:
Para calcular o momento:
Um ponto já foi. Agora vamos para o outro...
Passo 4
Fazendo o corte no ponto ficamos com o segmento :
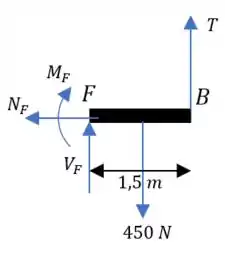
Fazendo essa bobeira toda que fizemos no passo anterior.
Somatório de força em :
Somatório de força em :
Momento:
Ufaaa... acabamos essa. Bora pra próxima?