Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 60
O hemisfério homogêneo do problema 5/42, cuja porção hemisférica central foi removida, está repetido aqui. Determine a coordenada do centro de massa usando o método desta seção.
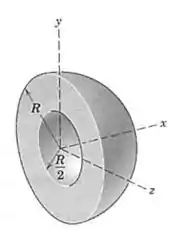
Passo 1
Galera, a gente foi abençoado pelos deuses da mecânica! Este problema é bem simples pra resolver, vamos dividir o problema em duas figuras, e fazer a subtração dos centroides! Vamos olhar de perfil!
Passo 2
Sabendo disso, vamos para os cálculos!!
Resposta
Exercícios de Livros Relacionados
Determine a altura h da abertura retangular na placa quadrada, que resultará em um centro de massa, para o restante da placa, o mais próximo possível da borda superior.
Determine a profundidade h do furo circular no cubo, para a qual a coordenada z do centro de massa terá o maior valor possível.
Determine a profundidade h do furo circular no cubo, para a qual a coordenada z do centro de massa terá o maior valor possível.
Determine a coordenada y do centroide da área sombreada. Use o resultado do problema 5/41.
Determine a coordenada y do centroide da área sombreada em função de h.