Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.4 - Ex. 56

Localize o centro de massa da barra esbelta dobrada na forma mostrada!

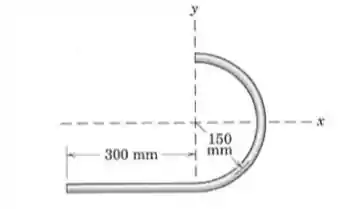
Passo 1

Sabendo que as equações para encontrar o centroide é dado por:

X - = ∑ x - L ∑ L

Y - = ∑ y - L ∑ L

Então precisamos descobrir esses elementos de L e x - e y - .

Passo 2

Para acharmos primeiro nosso L relacionado ao X, temos que lembrar que a nossa figura representa uma meia volta de uma circunferência no eixo da figura abaixo, logo:

L 1 = π   r = 150   π   m m

x - 1 = 2 r π = 300 π   m m

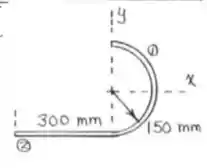
Temos então para a parte 2:

y - 1 = 0

L 2 = 300   m m

x - 2 = - 150   m m

y - 2 = - 150   m m

Passo 3

Agora fica bem simples gente, porque podemos voltar para nossa formula original de centroide a partir de área sem integral:

X - = ∑ x - L ∑ L = 300 π 150 π + 300   - 150 150 π + 300 = 0  

Y - = ∑ y - L ∑ L = 300 π 0 + 300   - 150 150 π + 300 = - 58.3   m m

Resposta

x - =   0

y - = - 58.3   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a coordenada y do centroide da área sombreada.
Determine as coordenadas x e y do centroide da área sombreada.
Determine as coordenadas do centroide da área trapezoidal mostrada.
Determine a coordenada y do centroide da área sombreada.
Determine a coordenada y do centroide da área sombreada. O triângulo é equilátero.