Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 123

Determine por integração direta os valores de x - para os dois sólidos obtidos passando-se um plano de corte vertical através da forma dada na figura 5.21. O plano de corte é paralelo a base da forma dada e divide-se em dois sólidos de mesma altura.

Um semielipsoide de revolução.

Passo 1

Bom galera, vamos começar separando o hemisfério em duas componente, assim:

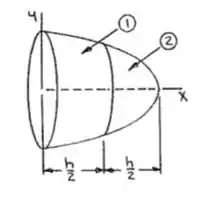
A gente pode deduzir que:

d V = π r 2 d x

E a equação geral dessa curva é:

x 2 h 2 + y 2 a 2 = 1

Logo:

r 2 = a 2 h 2 h 2 - x 2

Substituindo no que já tínhamos, fica:

d V = π a 2 h 2 h 2 - x 2 d x

Passo 2

Show de bola, agora a gente calcula os volumes de cada componente com uma integral:

V 1 = ∫ 0 h 2 π a 2 h 2 h 2 - x 2 d x = 11 24 π a 2 h

V 2 = ∫ h 2 h π a 2 h 2 h 2 - x 2 d x = 5 24 π a 2 h

E para podermos encontrar o centro de gravidade, também precisamos calcular:

x - 1 V 1 = ∫ 0 h 2 x π a 2 h 2 h 2 - x 2 d x = 7 64 π a 2 h 2

x - 2 V 2 = ∫ h 2 h x π a 2 h 2 h 2 - x 2 d x = 9 64 π a 2 h 2

Passo 3

Por fim, a gente calcula o centro de gravidade de cada componente:

x - 1 = 7 64 π a 2 h 2 11 24 π a 2 h = 21 88 h

x - 2 = 9 64 π a 2 h 2 5 24 π a 2 h = 27 40 h

Resposta

x - 1 = 21 88 h

x - 2 = 27 40 h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A caixa d’água AB tem tampa hemisférica e é construída com placas de aço finas. Determine o volume dentro da caixa.
Determine  a  área  da  superfície  externa  do  tanque.
Um  anel  é  gerado  ao  girar-se  a  área  de  um  quarto de círculo em torno do eixo x. Determine seu  volume.
Um anel é formado girando-se a área 360º em torno do eixo x – x . Determine sua área de superfície.
O tanque de processamento é usado para armazenar líquidos durante a manufatura. Estime a área  da superfície externa do tanque. O tanque tem topo plano e as placas com que é fabricado possuem espessur