Um anel é gerado ao girar-se a área de um quarto de círculo em torno do eixo x. Determine seu volume.
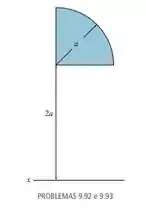
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão.
Primeiramente, devemos analisar o que será gerado. Girando este quarto de círculo, será gerada uma meia elipse, logo, basta achar o volume da elipse e dividir por 2. No entanto, deve-se retirar o retângulo formado no meio, de lados e . Logo:
O volume da elipse é dado por:
Portanto:
Mas deve-se retirar o retângulo: