Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 115
Determine o centro de gravidade mostrado na figura, sabendo que ela é feita de barras finas de latão o diâmetro uniforme.
Passo 1
Bom galera, o problema quer que a gente encontre o centro de gravidade do corpo da figura, que pode ser encontrada com essa fórmula básica do centroide:
A gente vai separar nossa chapa bem assim:
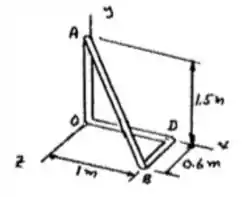
Passo 2
Show de bola, nós então montamos uma tabelinha simples com as áreas e os centroides de cada parte, esses centroides a gente encontrar lá no final do livro, então bora:
Passo 3
Então, a gente aplica aquela formula básica:
Resposta
Exercícios de Livros Relacionados
A parede de gravidade é feita de concreto. Determine a localização x - , y - do centro de massa G para a parede.
64. Localize o centroide y - da área da seção transversal da viga construída.
65. A placa composta é feita de segmentos de aço A e bronze B . Determine a massa e a localização x - , y - , z - de seu centro de massa G. Considere ρ a ç o = 7,85M g / m 3 ç e ρ b r = 8,74M g / m 3
Localize o centroide y - da área da secção transversal da viga construida.
Divida a placa em partes e, usando a grade para medição, determine aproximadamente a localização ( x - , y - ) do centróide da placa.