Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 137
Determine a intensidade da componente projetada da força que atua ao longo da linha .
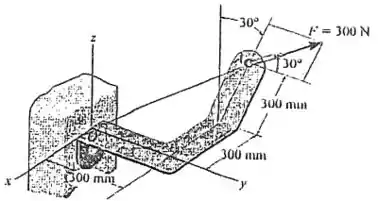
Passo 1
Para obter a componente desejada da força, o vetor força deve ser encontrado na sua forma vetorial a fim de ela poder ser dividida pelas suas componentes. Para tanto, deve-se fazer o produto escalar entre a força e o seu vetor unitário (lembre-se que o produto escalar entre uma constante e um vetor resulta em um vetor).
Ao final, para saber a componente basta realizar novamente o produto escalar. No entanto, isso será feito com o vetor unitário que direciona a linha .
Como dessa vez o produto escalar é entre dois vetores, o resultado será um valor constante.
Passo 2
Logo, o vetor unitário de será dado por:
E a força será:
E, portanto:
Passo 3
Agora, pode-se obter o vetor unitário da linha dado por:
Tal que:
Passo 4
Agora, fazendo o produto escalar com cada um dos dois vetores unitários é possível obter a componente que atua ao longo da linha :