Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas fundamentais - Ex. 17
Determine a intensidade da força hidrostática atuando por metro de comprimento da parede. A água tem densidade de
Passo 1
Falaaa! O problema pede que encontremos a intensidade da força hidrostática na parede submersa.
O que ele quer dizer com força atuando por metro de comprimento de parede, é que a gente só vai achar a força nesse plano, mas na verdade há muitos planos como esse ao longo do comprimento (entrando na tela) desse tanque.
Basicamente então queremos a força resultante do carregamento causado por esse fluído na parede. Esse carregamento é distribuído e tem o formato de um triângulo, assim:
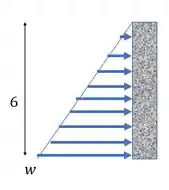
Como isso é uma carga distribuída, o que a gente precisa fazer é encontrar e calcular a resultante desse carregamento.
Passo 2
A gente precisa lembrar que a intensidade de carga que o fluido faz na parede na parte mais profunda é
Onde é a densidade da água, é a gravidade, é a profundidade de onde o fluído está e é aquele comprimento (entrando na tela) da parede.
Como a gente quer o valor da força por comprimento de parede, podemos dizer que . Aí o resultado sai como a gente quer.
Pela figura . A densidade o enunciado dá, e a gravidade a gente adota .
Beleza, então a gente já pode calcular a instensidade da carga de água:
Ou seja, temos um intensidade de carga de para cada metro de comprimento da parede.
Passo 3
Show de bola, pra gente calcular a força resultante total a gente calcula a área do triângulo que representa a distribuição de carga.
Ou seja, temos uma força resultante de para cada metro de comprimento da parede.