Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 6
O controle da haste exerce uma força sobre o setor circular, como mostrado. Determine os componentes de força em e .
Passo 1
Oooi!
Vamos começar a resolução desenhando o eixo e destacando o ângulo que faz com o eixo .
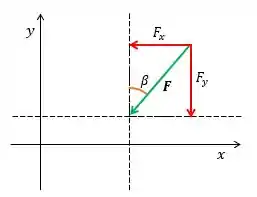
Depois de ilustrar, tudo fica mais fácil, né? Só precisamos identificar quem são as componentes e . Veja que o vetor aponta para o sentido negativo de e de , então,
Passo 2
Agora vamos desenhar o eixo (normal e tangente) e observar o ângulo que faz com o eixo .
As forças normal e tangencial são positivas e o ângulo que ele faz como o eixo é:
Sabendo disso, podemos identificar quem são as componentes e .
Resposta
Exercícios de Livros Relacionados
Determine os componentes F a e F b com a força de 4k N ao longo dos eixos oblíquos a e b . Determine as projeções de P a e P b de F sobre os eixos a e b .
A força F de 4k N é aplicada no ponto A . Calcule o momento F em relação ao ponto O , expressando-o como um escalar e como uma quantidade vetorial. Determine os pontos nos eixos x e y em relação aos q
A região lombar inferior A é a parte da coluna vertebral mais suscetível a abusos enquanto resistindo à flexão excessiva causada pelo momento de uma força F em relação a A . Para determinados valores
Determine o momento da tensão T em relação ao ponto P e ao ponto O .
Calcule o momento da força de 0,4l b em relação ao pivô O do disjuntor de parede.