Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 57
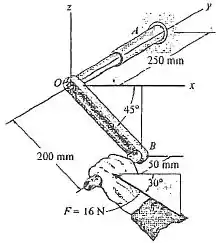
57. Determine a intensidade do momento que a força exerce sobre o eixo y da manivela. Resolva o problema usando uma abordagem de vetor cartesiano e usando uma abordagem escalar.
Passo 1
Primeiro vamos começar com a abordagem vetorial e tudo que ela precisa para ser usada, depois que terminarmos com ela vamos para abordagem escalar e a explicação para usá-la.
A distâncias na imagem estão em mm, mas vamos usá-las em m que é a unidade convencional.
Abordagem vetorial:
Para fornecer o resultado como o enunciado pede precisamos calcular o momento da força usando o produto vetorial que é dado da seguinte maneira:
Onde:
representam as componentes do vetor unitário definido na direção do eixo de rotação
representam as coordenadas do vetor posição definido a partir de qualquer ponto O sobre o eixo de rotação até qualquer ponto na linha de aplicação da força.
são as componentes da força aplicada.
O vetor mencionado acima pode ser visto na figura abaixo.
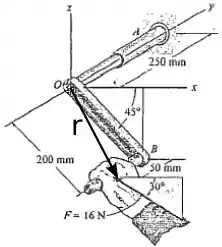
Para saber as coordenadas desse vetor, basta olhar a figura e ver quanto você tem que andar para cada direção para chegar ao ponto na linha de ação da força, logo:
O vetor unitário que tem a mesma direção que o eixo de rotação que é o eixo y, é dado por:
Passo 2
Agora precisamos separar nosso vetor força em suas componentes para podermos usá-las em nossas contas.
Pela forma que a força está sendo aplicada, só teremos componentes x e z da força. Essas componentes são dadas por:
E nossa é igual a zero.
é negativo pois aponta para o lado negativo de x.
Passo 3
Agora que já temos tudo que precisamos, vamos calcular o momento em relação ao eixo pedido.
Passo 4
Agora vamos resolver o problema usando análise escalar.
Análise escalar:
Para resolver esse exercício vamos usar o método de análise escalar que é baseado na fórmula:
Onde d nesse caso é a distância perpendicular do braço do momento a parti do eixo da linha da força.
No passo 2 já calculamos as componentes da força e vamos usá-las de novo
Com isso sabemos as três componentes da nossa força.
Vamos definir também o sentido positivo do momento conforme a regra da mão direita.
Passo 5
Temos que para o eixo de rotação, sendo o eixo y, a força na direção y não colabora para o momento ou produz qualquer tendência para girar já que ela é paralela ao eixo de rotação.
Os braços de momento referentes a cada força e que são perpendiculares a linha de ação de sua respectiva componente da força são:
Assim nosso momento em relação ao eixo de rotação y é:
Resposta
A intensidade do momento da força em relação ao eixo y é: