Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 50
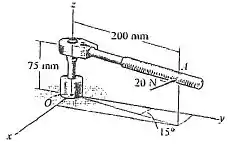
50. Uma força horizontal de é plicada perpendicularmente ao cabo da chave de soquete. Determine a intensidade e os ângulos de direção coordenados do momento criados por essa força em relação ao ponto O.
Passo 1
Para encontrar o resultado que o enunciado pede vamos calcular primeiro o momento da força F usando o produto vetorial que é dado da seguinte maneira:
Onde:
representam as coordenadas do vetor que vai da origem da rotação até o ponto de aplicação da força;
são as componentes da força aplicada.
O vetor mencionado acima pode ser visto na figura abaixo.
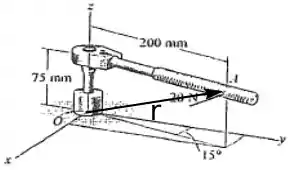
Para saber as coordenadas desse vetor, basta olhar a figura e ver quanto você tem que andar para cada direção para chegar ao ponto de aplicação da força, logo:
Para achar as componentes x e y do vetor acima, basta fazer:
Depois que fizermos todas essas contas, encontraremos o vetor momento, para achar a intensidade do momento basta calcular o módulo do vetor.
Para calcular os ângulos de direção coordenados, que nada mais é que os ângulos que o vetor momento faz com os eixos x, y e z, vamos lembrar que:
Como vamos interpretar isso para o nosso problema?
É o seguinte, para encontra o ângulo entre o vetor momento e um determinado eixo, basta pegar a componente do vetor em relação ao eixo que queremos e dividir pelo módulo do vetor.
Isso acontece pois sempre podemos formar um triângulo retângulo com o nosso vetor e um dos eixos. Mas para isso não vamos usar nosso vetor momento, entretanto vamos usar seu vetor direção.
Passo 2
Mas antes de começar a usar esse método, temos que notar que a nossa força não está expressa em forma cartesiana, mas como o problema nos fornece o ângulo de inclinação do braço onde é aplicada a força perpendicularmente a ele, podemos decompô-la em suas componentes em x, y e z.
A componente em z é 0 já que a força está sendo aplicada horizontalmente.
Para calcular as outras, vamos pensar um pouco, antes da chave ser deslocada 15° a força que é aplicada nela era paralela ao eixo x já que a força é perpendicular a chave, assim se andamos 15° com a chave, a força anda 15° em relação a x.
Agora vamos achar a componente em x:
A componente em y é:
Passo 3
Agora que já obtemos tudo que precisávamos, vamos calcular o momento em relação ao ponto A.
Calculando a intensidade do momento.
Passo 4
Para calcular os ângulos de direção coordenados, vamos primeiro calcular o vetor direção do momento e o módulo desse vetor, da seguinte maneira:
Passo 5
Agora vamos calcular o ângulo entre o vetor e o eixo x e chamaremos de .
Vamos calcular o ângulo entre o vetor e o eixo y e chamaremos de .
Calculando o ângulo entre o vetor e o eixo z e chamando de .
Resposta
A intensidade momento é:
Os ângulos coordenados são: